【微分】∂/∂x、∂/∂y、∂/∂z を極座標表示に変換
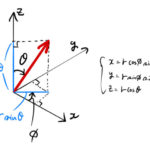
を で表すための計算をおこなう。これは、2階微分を含んだラプラシアンの極座標表示を導くときに使う。よくみる結果だけ最初に示す。 1階微分の極座標表示 1. 極座標表示 一般的な極座標変換 …
もっと読む 【微分】∂/∂x、∂/∂y、∂/∂z を極座標表示に変換バター猫のパラドックス

を で表すための計算をおこなう。これは、2階微分を含んだラプラシアンの極座標表示を導くときに使う。よくみる結果だけ最初に示す。 1階微分の極座標表示 1. 極座標表示 一般的な極座標変換 …
もっと読む 【微分】∂/∂x、∂/∂y、∂/∂z を極座標表示に変換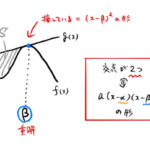
1/6公式、1/12公式などパターンをまとめた。大学入試でよく使った公式である。導出は数学Ⅲの部分積分を使わず、すべて数学Ⅱの積分レベルで工夫した。 (追い詰められた人向けの格言:面積を求める穴埋め問題なら、全部 絶対 …
もっと読む 【高校数学】面積を求める:1/6公式、1/12公式、1/30公式などパターンまとめ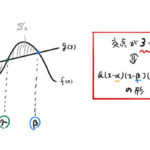
図の と の面積の和を求めたい。 ちなみに、 となるのは が三次関数の変極点になるとき。 1. 積分計算 3つ交点がある場合の面積を考えよう。交点の 座標をそれぞれ、 としておく。 2つの領域に分けてそれぞれの面 …
もっと読む 【積分】三次関数と直線が3交点をもつとき、囲まれた領域の面積の「和」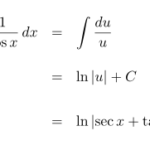
セカント(sec)の積分を計算する。この積分の形は の途中などに現れる。ここでは、うまい置換積分をすることで簡単に計算できる方法を紹介する。最終的な結果は下の通り。 sec(x)の不定積分 …
もっと読む 【積分】∫sec(x) dx(∫1/cos(x) dx)の不定積分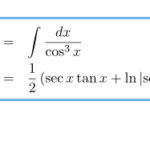
セカント(sec)の3乗、すなわち、1/cos の3乗の積分を計算する。うまい変形をすることで解ける。最終的な結果は以下の通り。 結果 1. 証明 に慣れてない人用に、 の形を使わずに …
もっと読む 【積分】∫sec^3(x) dx(∫1/cos^3(x) dx)の積分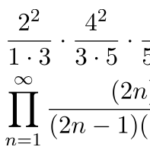
ウォリスの公式(Wallis formula)は無限積が になるという 驚きの結果である。 証明には、ウォリスの積分(Wallis’s integral)を使う。ウォリスの「積分」とウォリスの「公式」を混同 …
もっと読む 【積分】ウォリスの積分/ウォリスの公式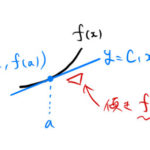
まわりのテイラー展開は となる。これの意味やイメージをまとめておく。 難しくないので簡単にまとめておく。 1. テイラー展開の意味とイメージ なぜ展開するのか? テイラー展開する理由は、式の見 …
もっと読む 【テイラー展開】かんたんな意味とイメージだけ伝える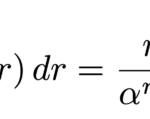
気体分子論や量子力学など物理でよく出てくる積分をまとめておく。その簡単な導出方法も示しておく。 ポイント ここで、 は負でない整数とする。 と積分変数を変換すれば、ガンマ関数を用いて計算がで …
もっと読む 【積分公式】∫r^n exp(-αr)dr (0→∞)