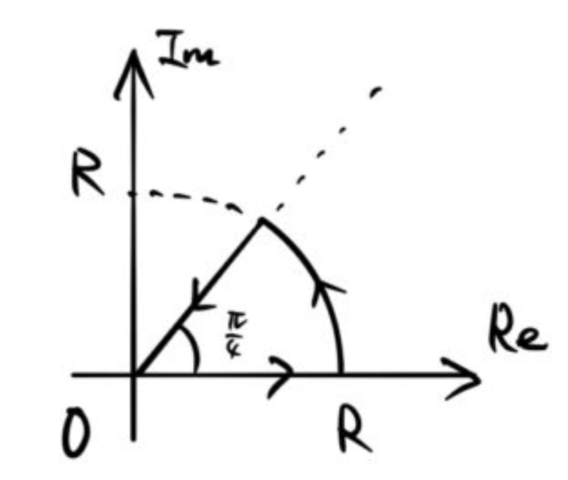
セカント(sec)の積分を計算する。この積分の形は ![]() の途中などに現れる。ここでは、うまい置換積分をすることで簡単に計算できる方法を紹介する。最終的な結果は下の通り。
の途中などに現れる。ここでは、うまい置換積分をすることで簡単に計算できる方法を紹介する。最終的な結果は下の通り。
sec(x)の不定積分
![]()
1. 証明
計算のポイントは、
- 分母分子に同じものをかける
- 置換積分を行う
ことである。以下はsecを使うか使わないか、書き方の違いであるが同じ計算方法である。
1.1 1/sinを使う式
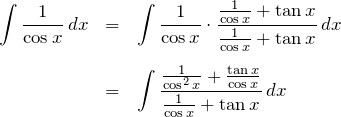
ここで、![]() とおくと、
とおくと、
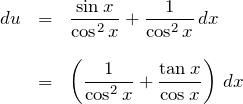
である。したがって、
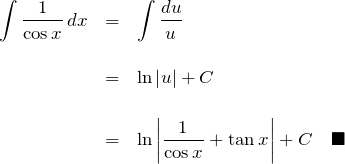
2.2 secを使う表式
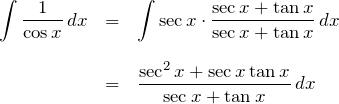
ここで、![]() とおくと、
とおくと、
![]()
である。したがって、
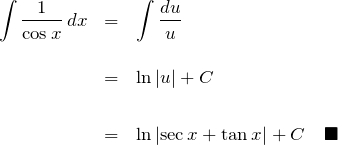
2. まとめ
分母分子に適当な関数をかけて、置換積分をおこなうことで簡単に計算できたと思う。よく出てくる変形なので覚えておきたい方法である。