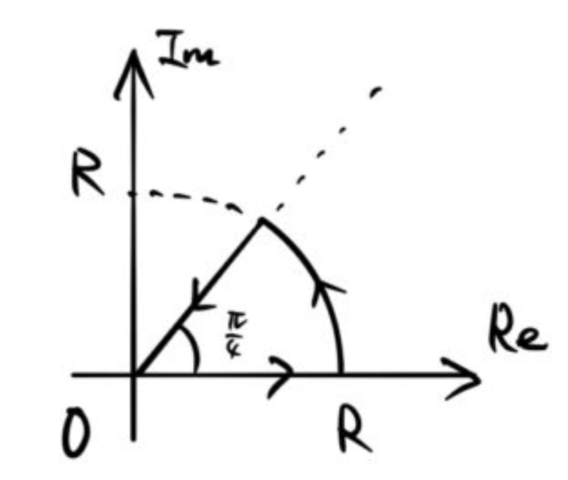
セカント(sec)の3乗、すなわち、1/cos の3乗の積分を計算する。うまい変形をすることで解ける。最終的な結果は以下の通り。
結果
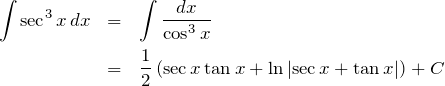
1. 証明
![]() に慣れてない人用に、
に慣れてない人用に、![]() の形を使わずに
の形を使わずに ![]() を使って変形していきます。ポイントは
を使って変形していきます。ポイントは
- 部分積分をうまく使う
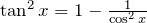 をうまく使う
をうまく使う
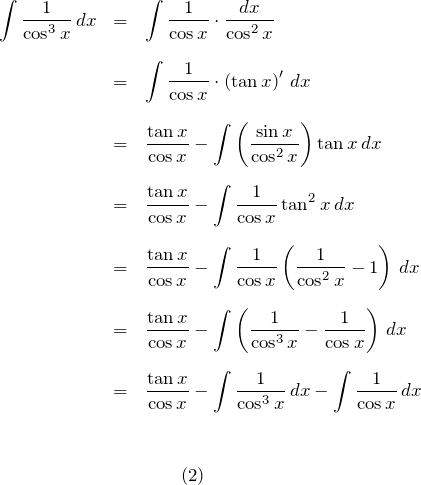
ここで、
![]()
を用いる。
また、右辺の被積分関数が ![]() の積分を右辺に移項する。
の積分を右辺に移項する。
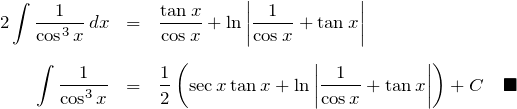
![]() とすれば、はじめに示した式と同じである。
とすれば、はじめに示した式と同じである。
2. まとめ
途中にあった
「部分積分→右辺と同じものが左辺に現れる」
のパターンは以下の積分のときにも見られる。
![]()
この積分は ![]() と置くことで求められる積分であり、途中式に
と置くことで求められる積分であり、途中式に ![]() が現れる。
が現れる。