二項定理
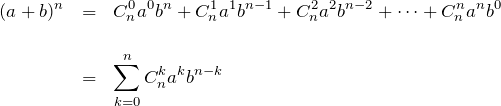
ここで、組み合わせ ![]() としている。上の二項定理を使えば和
としている。上の二項定理を使えば和 ![]() は
は ![]() の形に表すことができる。これを利用したさまざまな問題があるので、ここでは解き方とともに紹介する。
の形に表すことができる。これを利用したさまざまな問題があるので、ここでは解き方とともに紹介する。
二項定理を使ったいくつかの例題
次の式を和を用いない形に表せ。(![]() は自然数)
は自然数)
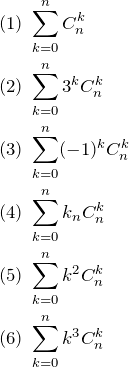
1. 解答
方針:二項定理の ![]() を何にすれば良いか考える。
を何にすれば良いか考える。
(1)の解答
【解答】 ![]() と置けば良い。
と置けば良い。
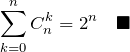
(2)の解答
【解答】 ![]() と置けば良い。(
と置けば良い。(![]() )
)
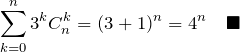
(3)の解答
【解答】 ![]() と置けば良い。
と置けば良い。
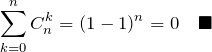
(4) の解答
【解答】![]() と置く。このとき、
と置く。このとき、
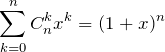
両辺を ![]() で微分して(
で微分して(![]() )、
)、
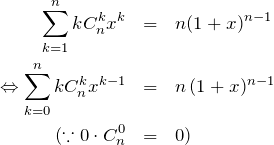
左辺の ![]() を利用するために、
を利用するために、![]() と置くと、
と置くと、
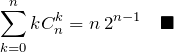
途中にできてきた ![]() を微分して使う方法は覚えておくと良い。
を微分して使う方法は覚えておくと良い。
ポイント
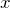 で微分して、
で微分して、
二項定理の公式において ![]() と置いた
と置いた
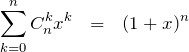
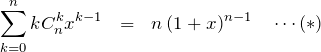
(5) の解答
【解答】式 (*) をさらに ![]() で微分して(
で微分して(![]() )、
)、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{d}{dx}\left[\sum_{k=0}^{n} k C_n^k x^{k-1}\right] &=& \frac{d}{dx}\left[n\,(1+x)^{n-1}\right]\\ \\ \Leftrightarrow \sum_{k=0}^{n} k(k-1) C_n^k x^{k-2} &=& n(n-1)\,(1+x)^{n-2} \quad \cdots (*)' \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9e941a4b336390098b553c3433d86824_l3.png)
となる。![]() を代入して、
を代入して、

![]() も含めた答えになる。
も含めた答えになる。
【補足】
右辺を展開して、(4)の結果を用いると以下の式を得る。
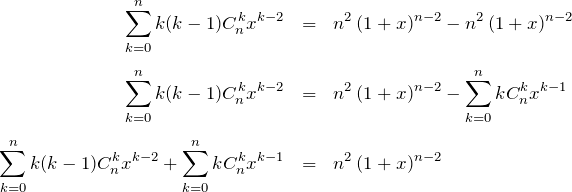
(6) の解答
【解答】(5)と同じように、式(*)’ を微分する
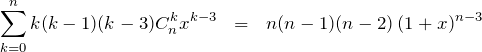
に ![]() を代入して、
を代入して、
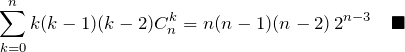
![]() のとき(
のとき(![]() )以上の場合でも同様にして微分していけば計算できる。ただし、
)以上の場合でも同様にして微分していけば計算できる。ただし、![]() の範囲は注意する。
の範囲は注意する。
2. まとめ
二項定理を使った計算をまとめた。ここにある例題は基本的に以下の2つの方針で計算することができる。
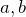 の値を決める
の値を決める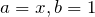 の二項展開に対して微分をうまく使う
の二項展開に対して微分をうまく使う
よくある二項定理の計算だが忘れがちなので確認しておきたい。