図の ![]() と
と ![]() の面積の和を求めたい。
の面積の和を求めたい。
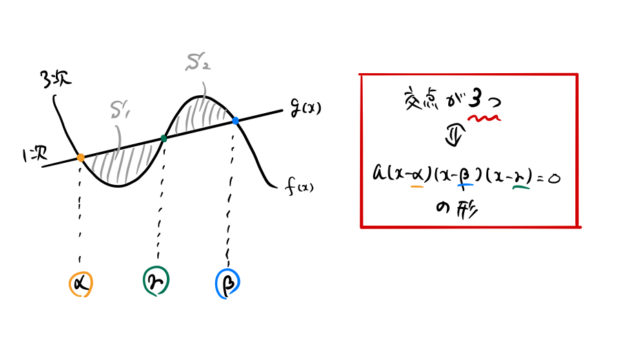
ちなみに、![]() となるのは
となるのは ![]() が三次関数の変極点になるとき。
が三次関数の変極点になるとき。
1. 積分計算
3つ交点がある場合の面積を考えよう。交点の ![]() 座標をそれぞれ、
座標をそれぞれ、![]() としておく。
としておく。

2つの領域に分けてそれぞれの面積 ![]() を求める。以下に注意する。
を求める。以下に注意する。
- 関数の差のもつ因数は、
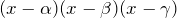
- (上の式)-(下の式)に注意
- 3次関数の
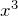 の係数は
の係数は  とする
とする
S1 について
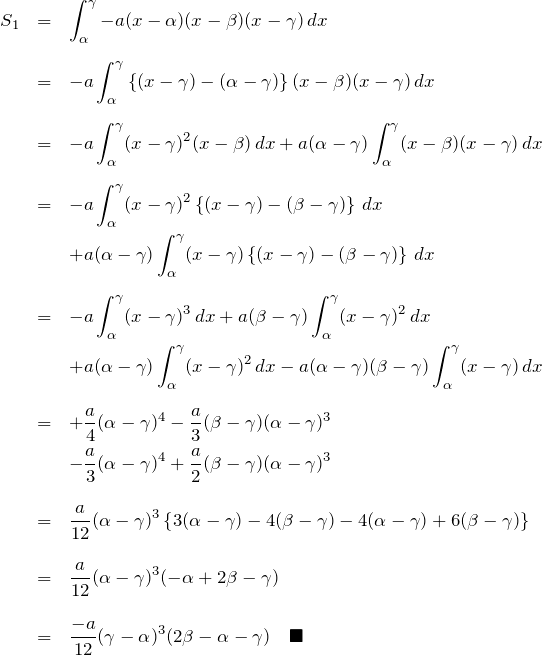
![]() 、
、![]() より面積
より面積 ![]() になる。
になる。
![]() で いわゆる1/12公式になる。
で いわゆる1/12公式になる。
S2 について
![]() の結果を利用する。
の結果を利用する。
- 積分区間
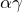 を
を 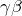 にする
にする - (上の式)-(下の式)を入れ替える(符号を逆にする)
途中(上の計算の5個目の等号)までは同じである。
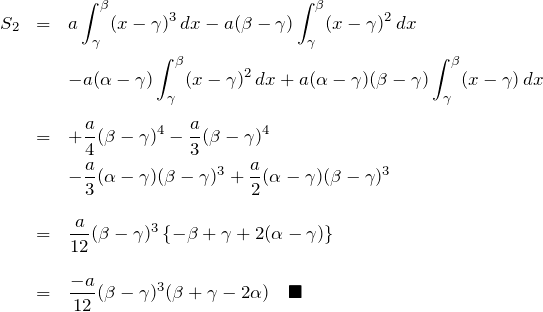
![]() と同じく
と同じく ![]() 、
、![]() より面積
より面積 ![]() になる。
になる。
![]() で いわゆる1/12公式になる。
で いわゆる1/12公式になる。
S1 + S2 の計算
![]() と
と ![]() 足すのはしんどいですね。
足すのはしんどいですね。
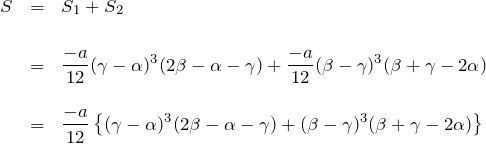
![]() と置くと、
と置くと、
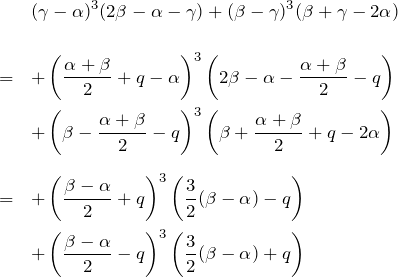
である。![]() と置くと、
と置くと、
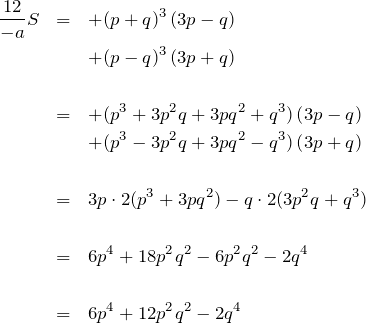
![]()
この答えを確かめるために、![]() とする。このとき、
とする。このとき、
![]()
であるので、
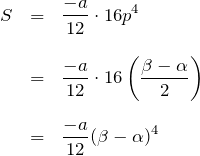
で 1/12公式に一致する。
![]() を使ったものを最終的な答えにしておこう。
を使ったものを最終的な答えにしておこう。
S1+S2の面積
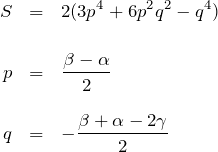
2. まとめ
これは公式やらあるのだろうか。