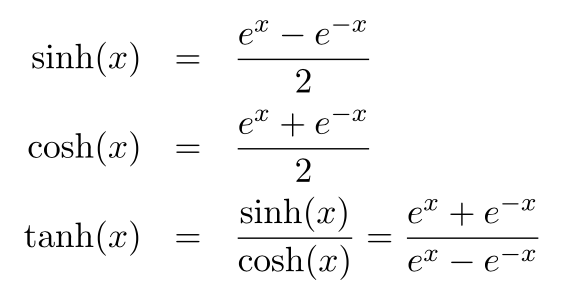![]() まわりのテイラー展開は
まわりのテイラー展開は
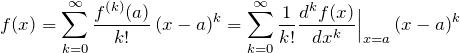
となる。これの意味やイメージをまとめておく。 難しくないので簡単にまとめておく。
1. テイラー展開の意味とイメージ
なぜ展開するのか?
テイラー展開する理由は、式の見通しをよくするためである。
とくに物理学で現象を数式で表現した時に、あまりに複雑であると現象の意味を捉えにくい。 例えば ![]() と展開して近似するだけで、直感的にわかりやすい直線として表すことができる。 運動方程式を立てたりしたときに、とりあえず
と展開して近似するだけで、直感的にわかりやすい直線として表すことができる。 運動方程式を立てたりしたときに、とりあえず ![]() が小さい時どのようになるか見たいときにテイラー展開が大いに役立つ。
が小さい時どのようになるか見たいときにテイラー展開が大いに役立つ。
自分が関心のある位置や温度のまわりでテイラー展開することで、数式が扱いやすく見通しがよくなるのである。
ざっくりとしたイメージ
数式によるイメージは他で見る。ここでは絵だけでイメージを伝えよう。
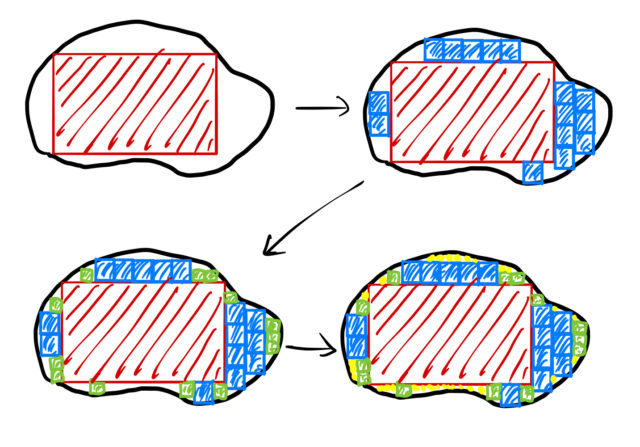
テイラー展開は、「複雑なものを簡単なもので展開」する。らくがきのような図の黒線で囲まれた図形も、いくつかの種類の四角形で近似的に表すことができる。
目的によって、どれくらいの精度で近似するか考える必要がある。大雑把に全貌を理解するのであれば、1次近似(大きな四角)のみを使えば良い。また、より細かく見たいなら高次の近似(細かい四角)を用意すれば良い。
* ここでいう次数というのは、![]() の次数
の次数 ![]() などのことである。
などのことである。
exp(x)の展開で見るイメージ
テイラー展開を文章で表すと、
複雑な関数 ![]() の
の ![]() の近くを、簡単な曲線で近似する
の近くを、簡単な曲線で近似する
ということである。![]() の
の ![]() まわりの展開を見ていこう。 簡単な曲線というのは1次関数の直線であったり2次関数の放物線であったりする。
まわりの展開を見ていこう。 簡単な曲線というのは1次関数の直線であったり2次関数の放物線であったりする。
まず1次、2次、3次関数による展開を見ていこう。 図は ![]() の領域について展開した様子である。
の領域について展開した様子である。
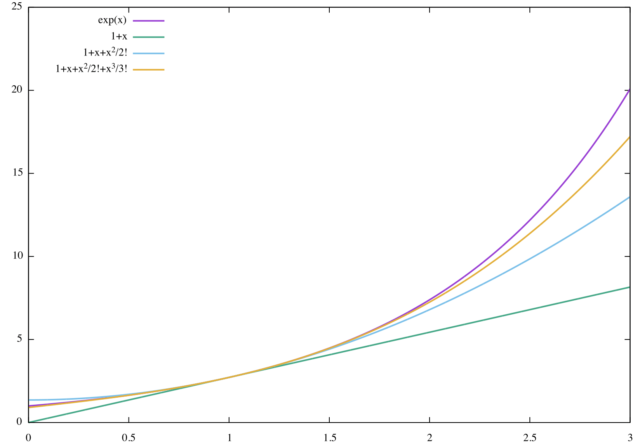
![]() のまわりで展開した直線は
のまわりで展開した直線は ![]() のまわりでよく一致する。 しかし、
のまわりでよく一致する。 しかし、![]() から離れると
から離れると ![]() との「ズレ」が大きくなる。 それに比べて、2次関数や3次関数では
との「ズレ」が大きくなる。 それに比べて、2次関数や3次関数では ![]() から「ズレ」ても1次関数よりは
から「ズレ」ても1次関数よりは ![]() に近い。
に近い。
より高次の関数まで使えば、もともとの関数をうまく近似できる。 つぎに ![]() の範囲で、より10次関数まで近似した場合を示す。
の範囲で、より10次関数まで近似した場合を示す。
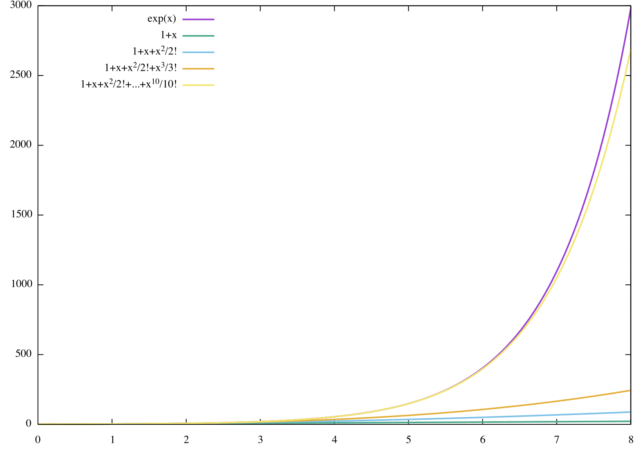
10次関数は1次、2次、3次に比べて範囲で近似できている。
この結果から「なんでもかんでも高次までとればいい」と考えるのは早計である。 なぜなら、テイラー展開を使う目的は、考えている ![]() 周りでの数式を単純なものに近似して見通しをよくすることであるからだ。
周りでの数式を単純なものに近似して見通しをよくすることであるからだ。
また、近似式が出てきた時には、その近似がどの範囲まで妥当であるか考えるようにすることが重要である。
1次と2次の展開にみるイメージ
多くの場合、1次か2次までテイラー展開すれば十分である。
![]() で曲線
で曲線 ![]() を拡大してみよう。
を拡大してみよう。
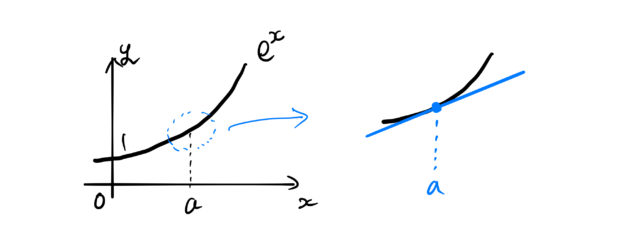
拡大すればするほど直線に近づいていくだろう。 この拡大した部分を直線で近似することを考える。
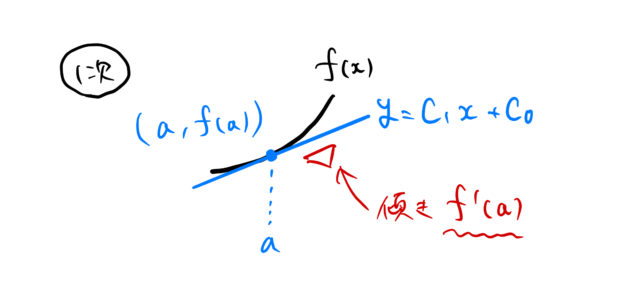
1次までのテイラー展開の形
![]()
によると、近似した直線の傾き ![]() と切片
と切片 ![]() は
は
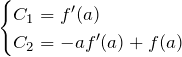
である。![]() は
は ![]() における曲線
における曲線 ![]() の接線の傾きに等しい。
の接線の傾きに等しい。
すなわち
1次で展開するとは、![]() 近傍の曲線を
近傍の曲線を ![]() の接線で近似すること
の接線で近似すること
である。 どんな曲線でも細かく見ていけば、直線に近似できるということである。
![]() から少し離れたところを見てみる。
から少し離れたところを見てみる。
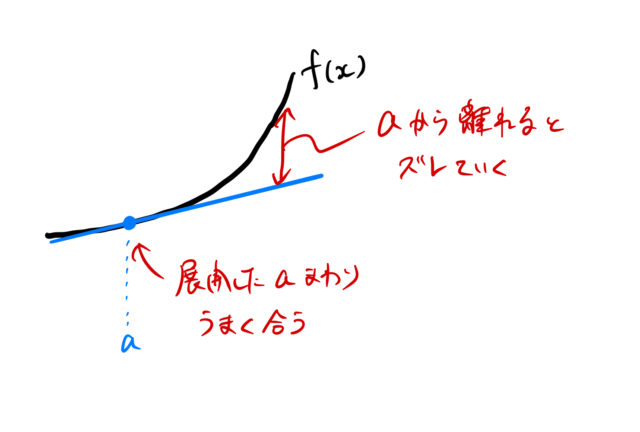
![]() の展開で見てきたように直線での近似は考えている点から離れれば、もとの曲線と全く異なるだろう。それでも、
の展開で見てきたように直線での近似は考えている点から離れれば、もとの曲線と全く異なるだろう。それでも、![]() 近くがどのように振る舞うのかを知るには十分である。
近くがどのように振る舞うのかを知るには十分である。
もっと正確に近似したい場合は2次まで近似すれば良い。 放物線で近似した場合は、直線よりも元の曲線をうまく近似できる。
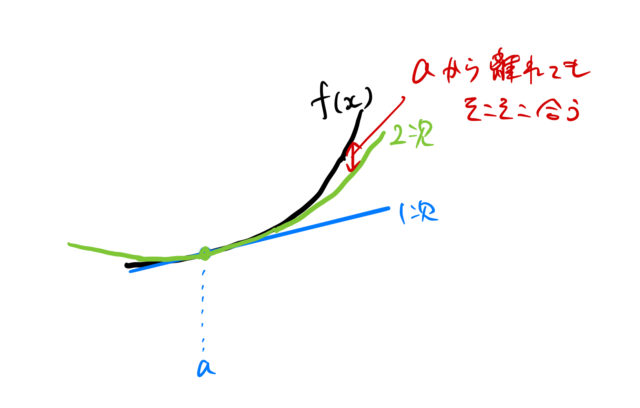
2. まとめ
ここではイメージをメインに伝えた。 テイラー展開における重要なことは
- 数式を理解しやすい形に近似できること
- 1次近似は接線での近似であること
である。あとは誤差など細かいことはあるが、上の2つはおさえておきたい。