ウォリスの公式(Wallis formula)は無限積が ![]() になるという 驚きの結果である。 証明には、ウォリスの積分(Wallis’s integral)を使う。ウォリスの「積分」とウォリスの「公式」を混同しないように注意する。ウォリスの公式は無限積なのでウォリス積とも呼ばれるが、ウォリスの積分と混同するためにここでは「ウォリスの公式」と呼ぶことにした。
になるという 驚きの結果である。 証明には、ウォリスの積分(Wallis’s integral)を使う。ウォリスの「積分」とウォリスの「公式」を混同しないように注意する。ウォリスの公式は無限積なのでウォリス積とも呼ばれるが、ウォリスの積分と混同するためにここでは「ウォリスの公式」と呼ぶことにした。
まず、最初にウォリスの積分 ![]() を定義しておく。
を定義しておく。
ウォリスの公式(Wallis formula)
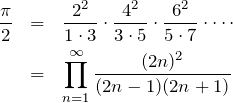
1. ウォリスの積分
ウォリスの積分は漸化式で表すことができる。以下のように sin と cos の ![]() 乗の積分で定義する。
乗の積分で定義する。
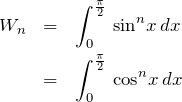
sin から cos への変換は ![]() と積分変換すればよい。
と積分変換すればよい。
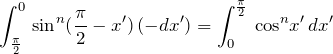
漸化式をみるために、積分していく。ポイントは3点。
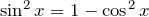 の利用
の利用- 部分積分の実行
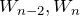 の形を作る。
の形を作る。
![]() に対して、
に対して、
![Rendered by QuickLaTeX.com \begin{eqnarray*} W_n &=& \int_{0}^{\frac{\pi}{2}}\, {\rm sin}^2 x \,{\rm sin}^{n-2} x\, dx \\ \\ &=& \int_{0}^{\frac{\pi}{2}}\, \left( 1-{\rm cos}^2 x\right) \,{\rm sin}^{n-2} x\, dx \\ \\ &=& \int_{0}^{\frac{\pi}{2}}\, {\rm sin}^{n-2} x\, dx - \int_{0}^{\frac{\pi}{2}}\, {\rm cos}^2 x\, {\rm sin}^{n-2} x\, dx \\ \\ &=& W_{n-2} - \int_{0}^{\frac{\pi}{2}}\, {\rm cos} x\left( \frac{1}{n-1} {\rm sin}^{n-1} x\right)'\, dx \\ \\ &=& W_{n-2} - \left[\frac{1}{n-1} {\rm cos}x\, {\rm sin}^{n-1} x\right]_{0}^{\frac{\pi}{2}} + \frac{1}{n-1} \int_{0}^{\frac{\pi}{2}}\, -{\rm sin} x\left( {\rm sin}^{n-1} x\right)\, dx \\ \\ &=& W_{n-2} + \frac{1}{n-1}W_{n} \\ \\ \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9ada2a0ee2e37833ee072bf80e0b5e2d_l3.png)
![]()
重要な ![]() と
と![]() に関する漸化式を得た。
に関する漸化式を得た。
ここで、![]() を計算する。
を計算する。
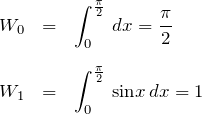
先ほどの漸化式を繰り返し使うが、![]() の偶数のときは最後が
の偶数のときは最後が ![]() になるし、
になるし、![]() の奇数のときは最後が
の奇数のときは最後が ![]() になる。したがって、
になる。したがって、![]() で場合分けをする。
で場合分けをする。
偶数(![]() ):
):
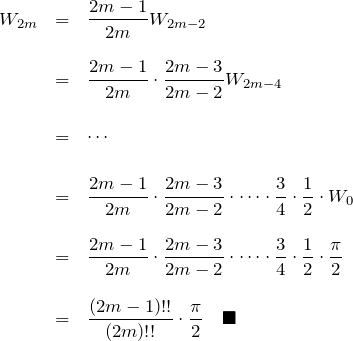
奇数(![]() ):
):
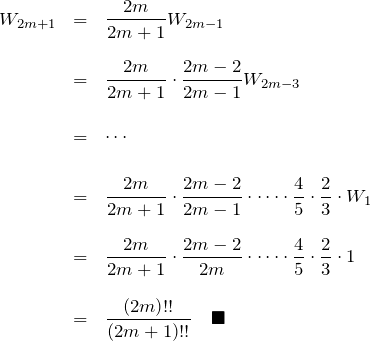
2 ウォリスの公式の証明
【証明】
![]() において、
において、
![]()
なので、![]() より、
より、
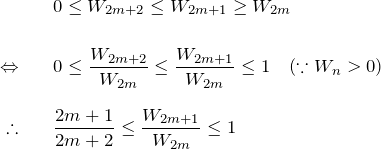
はさみうちの原理より、
![]()
ここで、
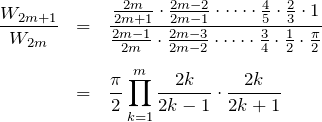
を代入して、
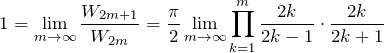
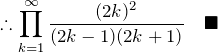
3. まとめ
ウォリスの積分は高校数学でもでてくる。アステロイドなどの回転体の体積を求める時に現れて知っておくと計算が早くできる。ガンマ関数との関連も書いていきたいところ。
検索結果は「ウォリス積」:709件、「ウォリスの公式」:15900件 であった。後者には漸化式の関係まで入っているかもしれないし、「ウォリス積」以外の公式も含まれている?