関数 ![]() に関するヒルベルト変換は以下で与えられる。
に関するヒルベルト変換は以下で与えられる。
![]()
例として、 デルタ関数的な周波数依存性を持つ関数 ![]() を考える。
を考える。
&=&\frac{1}{\pi}P\int_{-\infty}^{\infty}\frac{\pi\delta(\omega'-\varepsilon)}{\omega-\omega'} d\omega'\\&=&\frac{1}{\omega-\varepsilon}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4f27a02d77ec1a2ecbd42f73d2d99532_l3.png)
![]() のヒルベルト変換が
のヒルベルト変換が ![]() になるということは、
になるということは、 ![]() の逆ヒルベルト変換が
の逆ヒルベルト変換が ![]() になるということを意味する。したがって、
になるということを意味する。したがって、
![]()
のように2つはヒルベルト変換・逆変換で結ばれるヒルベルト変換対になる。
このようなヒルベルト変換対の関係は 、線形応答理論でよくみるクラマース・クローニッヒの関係において現れる。クラマース・クローニッヒの関係は、ある複素関数 ![]() の実部と虚部の関係を結ぶ。
の実部と虚部の関係を結ぶ。
実部と虚部の関係
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\rm Re}[F(\omega)] = + \frac{1}{\pi} P\int_{-\infty}^{\infty} \frac{{\rm Im}[F(\omega ')]}{\omega - \omega'} d\omega'\\ {\rm Im}[F(\omega)] = - \frac{1}{\pi} P\int_{-\infty}^{\infty} \frac{{\rm Re}[F(\omega ')]}{\omega - \omega'} d\omega' \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6136a64cc790a446627ca5db6fdedb77_l3.png)
この関係の有用性は、虚部から実部が求められたり、また逆に実部から虚部が求められることである。
例えば、![]() として 誘電関数(複素誘電率)
として 誘電関数(複素誘電率) ![]() を考えれば、光物性などの情報が得られる。(例えば、
を考えれば、光物性などの情報が得られる。(例えば、 ![]() は誘電損失を与える)
は誘電損失を与える)
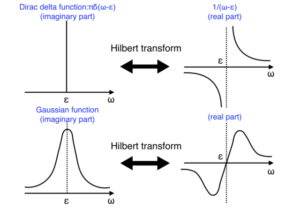
応用の上で、クラマース・クローニッヒの関係あるいはヒルベルト変換でデルタ関数がどうなるかを視覚的に捉えることも有用である。また、デルタ関数をガウス関数(ガウシアン)でブロードニングした場合についても同様に有用である。デルタ関数およびガウス関数のヒルベルト変換の概形を図に示した。