必要な前期量子論の知識
ボーアの量子化条件
電子の波長 ![]() と軌道半径
と軌道半径 ![]() の間に
の間に
![]()
量子化されている量はとびとびの値をとることである。 波長 ![]() は上のような条件を満たす必要があり、量子化されているという。
は上のような条件を満たす必要があり、量子化されているという。
上の量子化条件はボーアの量子化条件と呼ばれている。下の図はこの条件のイメージになる。
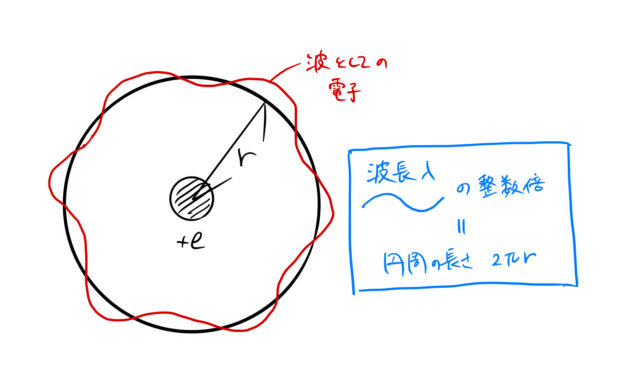
ド・ブロイの関係式
ところで、上の式は電子の波長 ![]() によって書かれている。 つまり、電子を「波動」として捉えているのである。
によって書かれている。 つまり、電子を「波動」として捉えているのである。
光が「粒子」と「波動」(波)の二重性を持つのと同様に、「粒子」であると考えられていた電子も「波動」としての性質を持つことが知られている。 さらにはあらゆる「粒子」として扱われているものには、「波」としての性質をもつと考えられている。
粒子の性質である運動量 ![]() と、波の性質である波長
と、波の性質である波長 ![]() の間にはド・ブロイの関係式
の間にはド・ブロイの関係式
![]()
ド・ブロイの式を用いると、ボーアの量子化条件を ![]() で書くことができる。波長
で書くことができる。波長 ![]() の代わりに、電子の速度
の代わりに、電子の速度 ![]() や運動量
や運動量 ![]() で書くと
で書くと
![]()
![]()
水素原子
水素原子は ![]() の電荷をもつ原子核と
の電荷をもつ原子核と ![]() の電荷をもつ電子で構成されている。このような水素原子において、電子の軌道がどのようになっているかを考え、対応する軌道半径やエネルギーを求めていこう。
の電荷をもつ電子で構成されている。このような水素原子において、電子の軌道がどのようになっているかを考え、対応する軌道半径やエネルギーを求めていこう。
計算のコツ
大したことではないが、ボーアの量子化条件を変形した
![]()
軌道半径
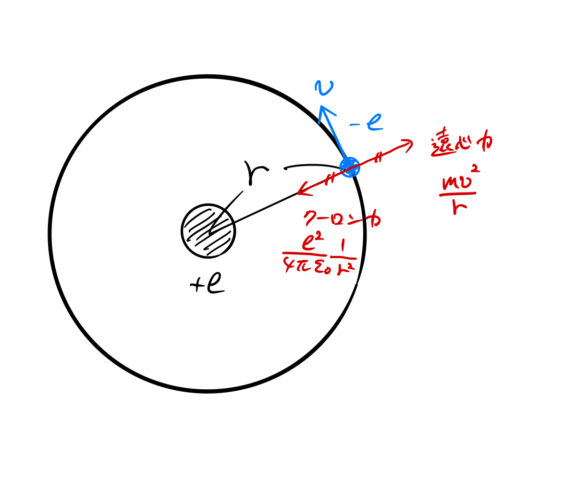
図のように軌道半径を ![]() とする。 電子はこの軌道を円運動しているとすると、古典力学の範囲で力の釣り合いの式を立てることができる。
とする。 電子はこの軌道を円運動しているとすると、古典力学の範囲で力の釣り合いの式を立てることができる。
この電子に働く力としては、「原子からのクーロン力」と「遠心力」のみである。それぞれ、
クーロン力(![]() は真空の誘電率):
は真空の誘電率):
![]()
遠心力:
![]()
が釣り合うので、
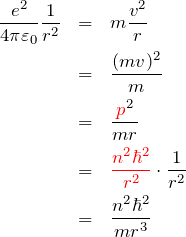
である。途中 ![]() として、ボーアの量子化条件
として、ボーアの量子化条件![]() を使いやすい形にしている。最後の式を
を使いやすい形にしている。最後の式を ![]() について解くと
について解くと
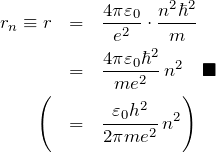
を得る(![]() により
により ![]() で表したものも括弧に書いておく)。
で表したものも括弧に書いておく)。 ![]() が整数で、
が整数で、![]() の係数に含まれる
の係数に含まれる ![]() は定数になるので、
は定数になるので、![]() は量子化されている。
は量子化されている。
このごちゃごちゃした係数(つまり ![]() )の値を
)の値を
![]()
* \AA(オングストローム)は、原子レベルの小さいスケールを扱うのに便利である。![]() を距離の単位にとる原子単位系もよく使われる。これは、地球と太陽の距離をau (天文単位)とするのと似ている。
を距離の単位にとる原子単位系もよく使われる。これは、地球と太陽の距離をau (天文単位)とするのと似ている。
結局、軌道半径 ![]() は
は
![]()
のように量子化されている。
量子化されたエネルギー
先ほどの図で、軌道半径が ![]() の場合の軌道エネルギー
の場合の軌道エネルギー ![]() を求める。速さ
を求める。速さ ![]() で円運動する電子の運動エネルギー
で円運動する電子の運動エネルギー ![]() とクーロンポテンシャル(静電ポテンシャル)
とクーロンポテンシャル(静電ポテンシャル)![]() (引力なので負)の和を計算すれば良い。
(引力なので負)の和を計算すれば良い。
運動エネルギーを、さきほどの![]() が出てくる形に式変形する。
が出てくる形に式変形する。
さきほどの力の釣り合いの式から、
![]()
の形を作っておく。したがって、軌道エネルギー ![]() は
は
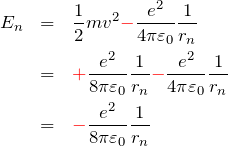
となる![]() 。 よって、さきほどの
。 よって、さきほどの ![]() の形を代入して
の形を代入して
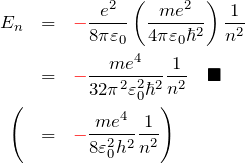
軌道半径 ![]() のときと同じく、軌道エネルギー
のときと同じく、軌道エネルギー ![]() も正数
も正数 ![]() によって量子化されている。ただし、
によって量子化されている。ただし、![]() に反比例したエネルギーになっていることに注意する。(エネルギーが負になっているのはクーロンポテンシャルが0となる点を無限遠(
に反比例したエネルギーになっていることに注意する。(エネルギーが負になっているのはクーロンポテンシャルが0となる点を無限遠(![]() )にとっていることによる。)
)にとっていることによる。)
ボーア半径 ![]() と同じく、
と同じく、![]() の係数のごちゃごちゃした部分
の係数のごちゃごちゃした部分
![]()
![]() を用いて水素原子の電子の軌道エネルギーを
を用いて水素原子の電子の軌道エネルギーを
![]()
と書ける。
[*]
2つの項をまとめる前の式で立ち止まってほしい。この式の第一項は運動エネルギーによる寄与で、第二項はクーロンポテンシャルによるエネルギーへの寄与である。クーロンポテンシャルが半径 ![]() が小さくなるほど、大きくなるのは正電荷と負電荷が近づくためである。一方で運動エネルギーに関しては、
が小さくなるほど、大きくなるのは正電荷と負電荷が近づくためである。一方で運動エネルギーに関しては、![]() により半径が小さいほど、電子は大きな
により半径が小さいほど、電子は大きな ![]() を持ち、不確定性原理が反映されている。
を持ち、不確定性原理が反映されている。
軌道エネルギー(原子単位系)
原子単位系(ハートリー単位系)は
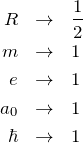
とした単位系である![]() 。これにより物理量を簡単な形で書くことができ、上で見てきたような文字だらけにならなくて済む。その反面、何の単位を扱っているかわかりにくくなることもあるので注意する。
。これにより物理量を簡単な形で書くことができ、上で見てきたような文字だらけにならなくて済む。その反面、何の単位を扱っているかわかりにくくなることもあるので注意する。
原子単位系で上で求めた軌道エネルギーを書くと
![]()
のようなシンプル表式になる。 ついでに軌道半径も原子単位系で
![]()
となる。
[*] リドベルグ定数 ![]() は、
は、![]() ととると自動的に
ととると自動的に ![]() となる。つまり
となる。つまり
![]()
より、
![]()
である。よって
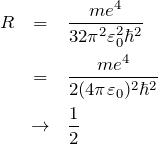
となる。
[**] 慣れないうちは、原子単位系を無理に使おうとしないで、![]() などを書いおいた方が安心である。ただし、教科書によっては原子単位系が使われているため、ハミルトニアンが
などを書いおいた方が安心である。ただし、教科書によっては原子単位系が使われているため、ハミルトニアンが ![]() でもびっくりしないこと。
でもびっくりしないこと。