時間 ![]() と位置
と位置 ![]() に依存する波の式
に依存する波の式 ![]() は波の特徴である波長
は波の特徴である波長 ![]() と周期
と周期 ![]() によって
によって
![]()
のように表すことができる。![]() は波の振幅である。 この式は波数
は波の振幅である。 この式は波数 ![]() と 周波数(角振動数)
と 周波数(角振動数) ![]() により
により
![]()
とも書ける。ここでは、この波の式を導出していく。 ![]() の係数が負になることに注意し、その理由も書いておく。
の係数が負になることに注意し、その理由も書いておく。
式の導出
波を
![]()
波を図示する
波 ![]() は
は ![]() と
と ![]() の関数になっているため
の関数になっているため
- 縦軸
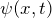 、横軸
、横軸 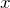
- 縦軸
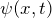 、横軸
、横軸 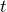
の2通りの描き方がある。要するにある時刻での空間変化について描くか、ある位置での時間変化について描くかの2通りである。
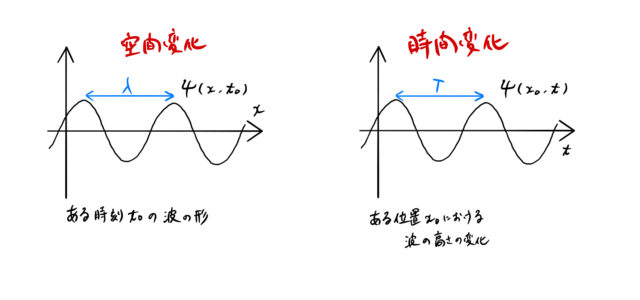
空間変化はイメージしやすく、海の細波を撮った写真を思い浮かべればよい。 横軸が変位 ![]() で表すことができるためわかりやすい。 山と山の空間的な間隔を波長
で表すことができるためわかりやすい。 山と山の空間的な間隔を波長 ![]() と呼ぶ。
と呼ぶ。
一方で、現実に横軸に時間をとって「見る」こと、つまり時間変化を「見る」のは難しい。 時間変化を見るためには、波のある位置 ![]() の高さがどのように変化していくかを記録していくしかない。 もっと簡単に時間変化を見るための装置がオシロスコープである。 山と山の時間的な間隔を周期
の高さがどのように変化していくかを記録していくしかない。 もっと簡単に時間変化を見るための装置がオシロスコープである。 山と山の時間的な間隔を周期 ![]() と呼ぶ。
と呼ぶ。
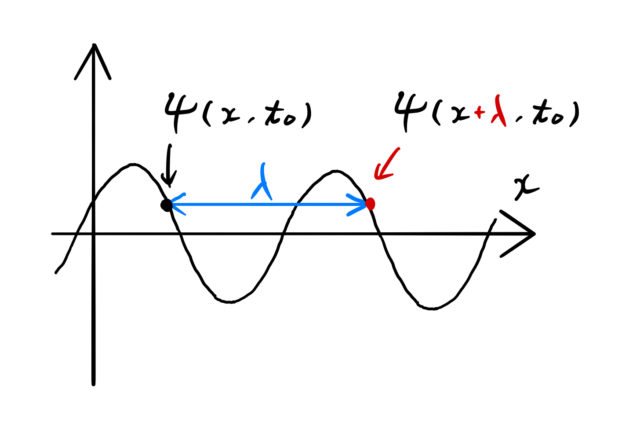
aを求める:時間tを固定する
![]() で固定して考える。
で固定して考える。
![]()
![]()
が成立する。
左辺を加法定理で展開していく。
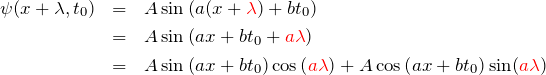
式(1)より
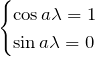
が成立する。したがって、
![]()
となる。![]() は整数であるが、
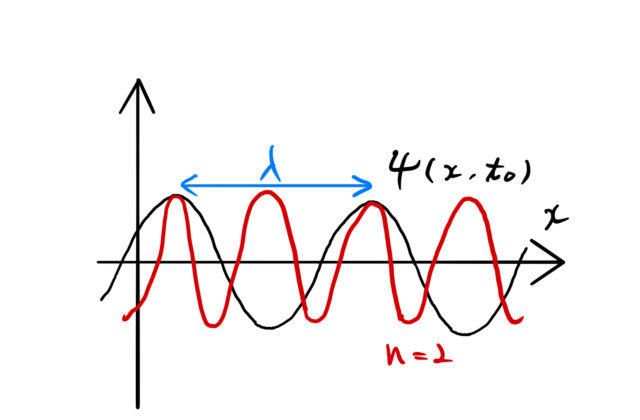
は整数であるが、![]() が目的の波の式である。 たとえば、
が目的の波の式である。 たとえば、![]() などは図のような波を表している。
などは図のような波を表している。
![]()
の条件だけでは、波の形は ![]() の値によって変化してしまう。
の値によって変化してしまう。 ![]() の間に、いくらでも山の数を詰め込むことができるのである。
の間に、いくらでも山の数を詰め込むことができるのである。
![]() のときを考えて、
のときを考えて、
![]()
*【指数関数で見る】
指数関数を用いて波を表すと、三角関数の加法定理の代わりに、指数関数の指数法則を用いるだけで済む。つまり、計算が簡単になる利点がある。
波を指数関数で表すと、
![]()
になる。
![]()
![]()
となる。したがって、
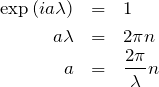
bを求める:位置xを固定する
時間を固定した場合と同様の計算をおこなうと、
![]()
を得る。ここで ![]() は整数である。
は整数である。 ![]() を決めたときと同様に
を決めたときと同様に ![]() であるように思える。
であるように思える。
しかし、波の進行方向を ![]() が正の方向である図のような場合を考えると
が正の方向である図のような場合を考えると ![]() となる。
となる。
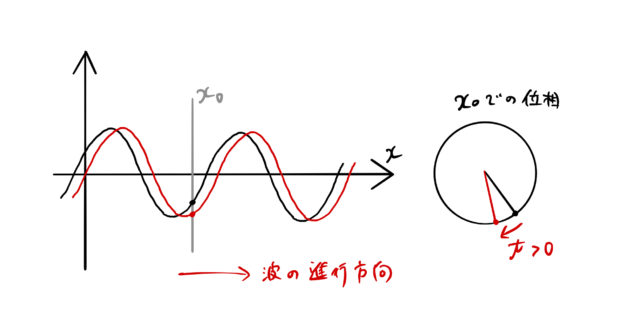
この図において、ある波の位置 ![]() について時間変化を追っていくことを考える。 ある時刻の状態から、時間
について時間変化を追っていくことを考える。 ある時刻の状態から、時間 ![]() だけ経過したときに
だけ経過したときに ![]() での波の位相(
での波の位相(![]() の中身)は、
の中身)は、![]() に対して負の方向に変化する。
に対して負の方向に変化する。
これでは少々粗いので、具体的に時刻が ![]() (
(![]() は微小)に変化した場合の式を見ていく。 このとき、初期状態と
は微小)に変化した場合の式を見ていく。 このとき、初期状態と![]() のときの波の式はそれぞれ、
のときの波の式はそれぞれ、
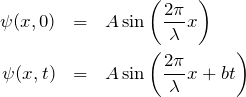
となる。
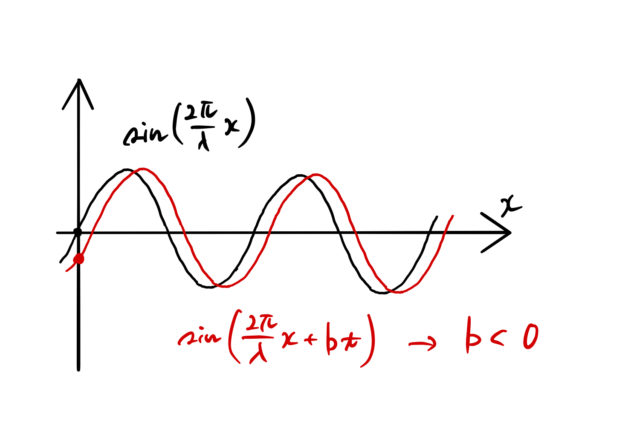
![]() での波の高さを見ていくと、
での波の高さを見ていくと、
![]()
となるだろう。いま、![]() 軸の正の方向へ進行する波(図の赤い線)の場合は
軸の正の方向へ進行する波(図の赤い線)の場合は ![]() であるため、
であるため、![]() の中身は負になるはずである。
の中身は負になるはずである。 ![]() であるため、
であるため、![]() にならざるを得ない。
にならざるを得ない。
これにより ![]() であり、
であり、
![]()
負の方向へ進む波
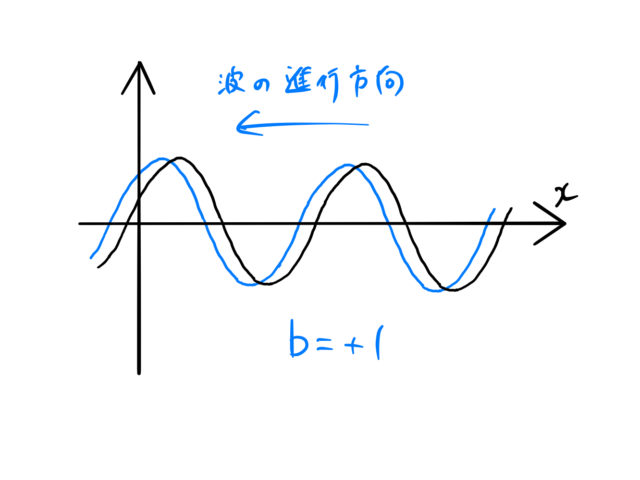
また、図のように ![]() は
は ![]() 軸の負の方向へ後退する波を表す。
軸の負の方向へ後退する波を表す。
まとめ
以上まとめて
![]()
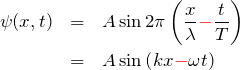
となる。![]() の係数は負になることに注意する。
の係数は負になることに注意する。
![]() 軸の負の向きへ後退する波の式は、
軸の負の向きへ後退する波の式は、
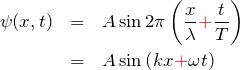
となる。![]() の係数は正になることに注意する。
の係数は正になることに注意する。