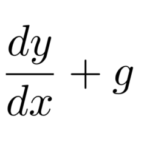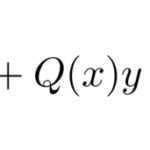基本的な流れ:
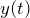 に関する積分方程式をラプラス変換
に関する積分方程式をラプラス変換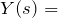 の形に変形(部分分数分解など)
の形に変形(部分分数分解など)- ラプラス逆変換で
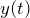 を求める
を求める
例題
![]() で定義された実関数
で定義された実関数 ![]() を考えて、以下の積分方程式をラプララス変換を用いて解け。
を考えて、以下の積分方程式をラプララス変換を用いて解け。
![]()
予備知識:
・積分のラプラス変換 (導出 ) ![]()
・![]() のラプラス変換
のラプラス変換
![]()
・![]() のラプラス変換
のラプラス変換
![]()
【解答】
![]() のラプラス変換を定義する。
のラプラス変換を定義する。
![]()
ここで、積分方程式の両辺をラプラス変換する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&{\mathcal L}\left[y(t)\right]={\mathcal L}\left[t\right](s)+{\mathcal L}\left[\int_0^{t}y(\tau)d\tau\right]\\\\ \Leftrightarrow&&Y(s)=\frac{1}{s^2}+\frac{Y(s)}{s}\\\\ \Leftrightarrow&& Y(s)=\frac{1}{s(s-1)}=\frac{1}{s-1}-\frac{1}{s} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-fa89d36352d7344e0d1afd4f6fc9fd9a_l3.png)
ラプラス逆変換すれば、
\\\\ &=&{\mathcal L}^{-1}\left[\frac{1}{s-1}\right] -{\mathcal L}^{-1}\left[\frac{1}{s}\right]\\\\ &=& e^t -1\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a7b4a00d7c8638540a26255ccd393870_l3.png)
ラプラス変換を使わない別解:
積分方程式の両辺を ![]() で微分する。
で微分する。
![]()
となり、簡単な微分方程式を得る。これは変数分離形で簡単に解ける。
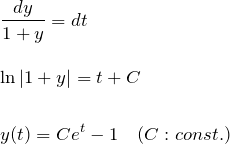
定数 ![]() を得るために、元の積分方程式において
を得るために、元の積分方程式において ![]() を代入して、
を代入して、
![]()
である。したがって、![]() を得る。
を得る。
![]()