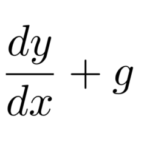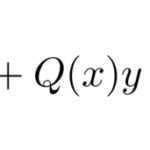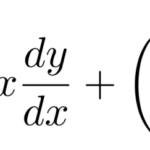以下のベルヌーイ型と呼ばれる微分方程式(Bernoulli differential equation)の解法を説明する。 特徴は、左辺は線形型に見えるが右辺に ![]() が含まれることである。
が含まれることである。
![]()
このタイプは ![]() とおけば線形型に帰着して解くことができる。 解き方を学び、例題を使ってベルヌーイ型を攻略しよう。
とおけば線形型に帰着して解くことができる。 解き方を学び、例題を使ってベルヌーイ型を攻略しよう。
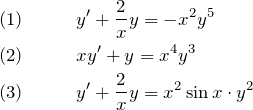
1. ベルヌーイ型の構造
![]()
について ![]() とおけば解ける理由やその発想の経緯を追っていこう。 ここは、「とにかく問題だけ解ければ良い」という方は飛ばしてもらって良い。
とおけば解ける理由やその発想の経緯を追っていこう。 ここは、「とにかく問題だけ解ければ良い」という方は飛ばしてもらって良い。
線形型に帰着することを確認する
![]() によってベルヌーイ型は線形型に帰着する。
によってベルヌーイ型は線形型に帰着する。
このことを確かめておこう。
両辺を微分して
![]()
となる。したがって、![]() を作るために もとの微分方程式の両辺に
を作るために もとの微分方程式の両辺に ![]() をかける。
をかける。
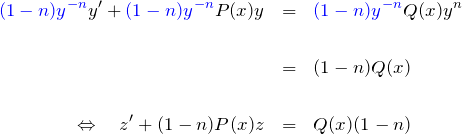
たしかに線形型に帰着する。これの一般解は
![]()
であった。これを覚えてはならないという話は、以前で説明した通りである。 覚えてもどうせ間違うので、線形型の一般解は導けるようにしておくべきである。
* ![]() に直すためには
に直すためには
![]()
としておけば良い。
この変数変換はどこから?
![]() の変換がどこからやってきたかを簡単に説明しておく。
の変換がどこからやってきたかを簡単に説明しておく。
![]()
について、![]() のときは線形型なので解くことができる。
のときは線形型なので解くことができる。
ベルヌーイ型 → 線形型
とするために、じゃまになっているのは ![]() である。 なんとか適当な変数変換により
である。 なんとか適当な変数変換により ![]() を消してしまいたいのである。
を消してしまいたいのである。
![]() の形でうまくいくかチェックしよう。
つまりこの変数変換により、「線形型」や「変数分離型」などよく知られたパターンに落とし込めるかを考える。
の形でうまくいくかチェックしよう。
つまりこの変数変換により、「線形型」や「変数分離型」などよく知られたパターンに落とし込めるかを考える。
![]()
であるため、
微分方程式の両辺に ![]() をかけて
をかけて
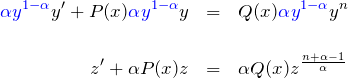
となる。
左辺が線形型に似ているものの、右辺に ![]() があり線形ではない。したがって、右辺の
があり線形ではない。したがって、右辺の ![]() を消すために
を消すために
![]()
とすればよい。このように ![]() をおくと、右辺の
をおくと、右辺の ![]() は消えて微分方程式は線形型に帰着するのである。
は消えて微分方程式は線形型に帰着するのである。
そういうわけで ![]() とおけば良い。
とおけば良い。
解法まとめ
ベルヌーイ型の微分方程式が解けるかどうかは、初めの変数変換の仕方を覚えているかどうかで決まる。以下、ベルヌーイ型の解法をまとめておく。
ベルヌーイ型の微分方程式
![]()
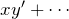 などの形なら
などの形なら 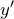 の形にしておく
の形にしておく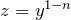 とおく
とおく- 上を両辺を
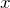 で微分:
で微分: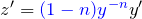
- 微分方程式の両辺に
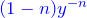 をかけて、
をかけて、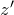 をつくる
をつくる - 線形型に帰着するため、
 に関する微分方程式を解く
に関する微分方程式を解く 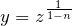 によって
によって 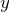 の形に直す
の形に直す
2. 例題の解答
以下、![]() は定数である。 線形型を解くときは「公式を覚えず解く1次線形型微分方程式」の流れで解いている。 各自自分の方法が解きやすい方法で解くのが良い。
は定数である。 線形型を解くときは「公式を覚えず解く1次線形型微分方程式」の流れで解いている。 各自自分の方法が解きやすい方法で解くのが良い。
例題(1)の解答
![]()
のベルヌーイ型。
![]() とおき、微分する。
とおき、微分する。
![]()
![]() をつくるため、微分方程式の両辺に
をつくるため、微分方程式の両辺に ![]() をかける:
をかける:
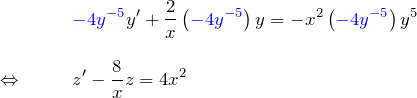
の線形型に帰着する。 次に、線形型を解いていく。
両辺にかけるもの:
![]()
微分方程式の両辺に ![]() をかける:
をかける:
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{1}{x^8}z'-\frac{8}{x^9}z=\frac{4}{x^6}\\\\ \Leftrightarrow \quad&&\frac{d}{dx}\left[\frac{z}{x^8}\right]=\frac{4}{x^6}\\\\ \Leftrightarrow \quad&& \frac{z}{x^8}=\int \frac{4}{x^6}\,dx=-\frac{4}{5}x^{-5}+C\\\\ \Leftrightarrow \quad&& z=-\frac{4}{5}x^3+Cx^8 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-7e43f7aef8fe6655462b6e95cf08ed95_l3.png)
![]() の形にもどす:
の形にもどす:
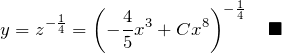
*答えは下の形でもよい。
![]()
例題(2)の解答
![]()
を変形して
![]()
のベルヌーイ型である。
![]() とおき、微分する。
とおき、微分する。
![]()
![]() をつくるため、微分方程式の両辺に
をつくるため、微分方程式の両辺に ![]() をかける:
をかける:
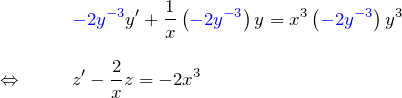
の線形型に帰着する。
次に、線形型を解いていく。
両辺にかけるもの:
![]()
微分方程式の両辺に ![]() をかける:
をかける:
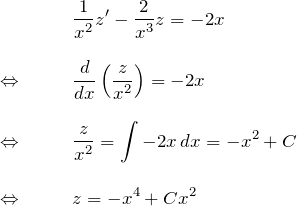
![]() の形にもどす:
の形にもどす:
![]()
* 答えは下の形でも良い。
![]()
例題(3)の解答
![]()
のベルヌーイ型。
![]() とおき、微分する。
とおき、微分する。
![]()
![]() をつくるため、微分方程式の両辺に
をつくるため、微分方程式の両辺に ![]() をかける:
をかける:
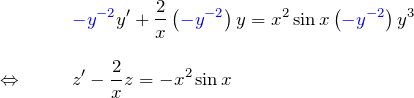
の線形型に帰着する。
次に、線形型を解いていく。
両辺にかけるもの:
![]()
微分方程式の両辺に ![]() をかける:
をかける:
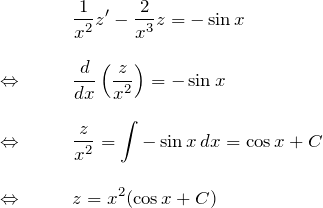
![]() の形にもどす:
の形にもどす:
![]()
* 答えは下の形でも良い。
![]()
3. まとめ
ベルヌーイ型の微分方程式を解いてきた。 ![]() の置き方さえマスターしておけば、あとはなんとでもなるだろう。 線形型に帰着するため、線形型の微分方程式の解き方は習得しておかなければならない。
の置き方さえマスターしておけば、あとはなんとでもなるだろう。 線形型に帰着するため、線形型の微分方程式の解き方は習得しておかなければならない。