【微分方程式】例題で学ぶ:全微分型(問題の見分け方/解法)
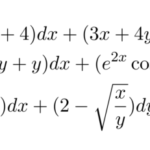
全微分型の微分方程式を解く。全微分型とは の形をしている。これは が分かれば簡単に解ける。 つまり、一般解は である。問題は「いかにして を求めるか」である。例題 …
もっと読む 【微分方程式】例題で学ぶ:全微分型(問題の見分け方/解法)バター猫のパラドックス
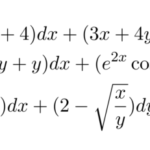
全微分型の微分方程式を解く。全微分型とは の形をしている。これは が分かれば簡単に解ける。 つまり、一般解は である。問題は「いかにして を求めるか」である。例題 …
もっと読む 【微分方程式】例題で学ぶ:全微分型(問題の見分け方/解法)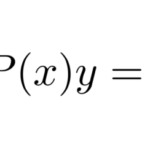
ここでの目的は、線形型の微分方程式 の解き方を習得し、例題を解けるようになることである。このタイプを解くには以下のコツだけ覚えていれば、後に示すような難しい一般解は不要になる。 ポイント 「 …
もっと読む 【微分方程式】公式を覚えず解く「1次線形型」の解法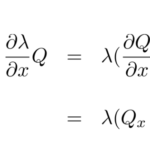
積分因子とは、与えられた微分方程式にかけて完全微分型の微分方程式を作るための因子である。 簡単に言えば、積分因子 を見つけることができれば微分方程式は完全微分型の微分方程式に帰着する。 ここでは、どのような仕組みで積 …
もっと読む 【微分方程式】積分因子の意味と完全微分型(例題で学ぶ)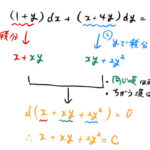
が完全微分型のときは のように変形できる。 したがって、(*)から(*)’を直接求めることができれば簡単に解くことができる。 すなわち、全微分される前の …
もっと読む 【微分方程式】ずるい完全微分型の解法(+例題15問)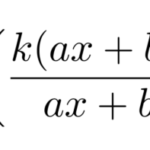
前回の続きから、同次型に似た例題を解いていこうと思う。 ここでは以下のタイプの微分方程式を「変数分離型」に帰着させることを目指す。 右辺の分子・分母をそれぞれ直線と見たとき、平行になる場合で …
もっと読む 【微分方程式】「同次型」に似た問題その(2)/u=ax+by+cと変換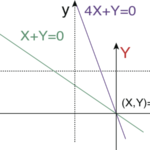
ここでは以下のような同次型に似た問題を扱う。 変数変換により同次型に帰着することがわかる。(同次型がわからない・解けない方は先に「同次型の解法」で解法を習得したほうがよいだろう。) 以下の …
もっと読む 【微分方程式】「同次型」に似た例題その(1)/平行移動による変数変換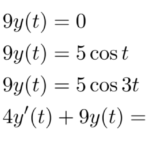
前回はラプラス変換を用いた斉次線形微分方程式を扱った。 ここでは例題を通して非斉次の線形微分方程式を解いていく。 例題(1)は斉次、(2)(3)(4)は非斉次の微分方程式である。 例題 次の に関する微分方程式を解け。 …
もっと読む 【例題で学ぶ】ラプラス逆変換(非斉次線形微分方程式)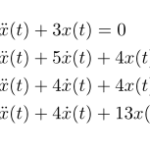
例題を使って微分方程式の初期値問題をラプラス変換で解く。 初期値が与えられている微分方程式はラプラス変換によってをかんたんに解くことができる。 ここでは下の例題のような単純な斉次線形微分方程式を解いていく(非斉次微分方 …
もっと読む 【例題で学ぶ】ラプラス逆変換(線形微分方程式の初期値問題)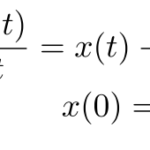
簡単な以下の微分方程式をラプラス変換を用いて解く。 【解答】 をラプラス変換した を定義する。 与えられた微分方程式の両辺をラプラス変換する。 世界 世界。 &nb …
もっと読む 【ラプラス変換】x’=x-t の初期値問題のラプラス変換による解法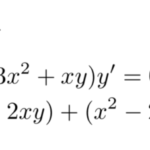
微分方程式の同次型は の形をとる。このタイプの微分方程式の解き方を例題を通して学習する。 同次型の例題 1. 同次型の微分方程式 同次型とは? 「同次」というのは次 …
もっと読む 【微分方程式】例題で学ぶ「同次型の微分方程式」の解法