【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型
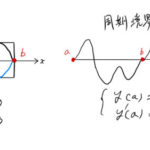
ステュルム-リウヴィル(Sturm-Liouville)型微分方程式 について見ていく。2階微分方程式であるので、解には2つの積分定数が現れる。 この微分方程式を解いて一般解を求めるのではな …
もっと読む 【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型バター猫のパラドックス

ステュルム-リウヴィル(Sturm-Liouville)型微分方程式 について見ていく。2階微分方程式であるので、解には2つの積分定数が現れる。 この微分方程式を解いて一般解を求めるのではな …
もっと読む 【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型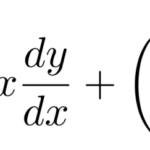
ダランベール型(ラグランジュ型)の微分方程式は以下の形をしている。 のときは、クレローの微分方程式である。 ここでは の一般的なラグランジュの微分方程式を見ていこう。 例題 次の微分方程式を …
もっと読む 【微分方程式】ダランベール型(ラグランジュ型)の解法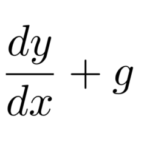
クレローの微分方程式は の形をしている。 ここではその解き方をまとめて、以下の例題を解けるようにする。包絡線と関係するので、そのことも簡単にまとめる。 よくわからないけど今すぐ解きたいという …
もっと読む 【微分方程式】例題で学ぶ:クレロー型/一般解・特異解/曲線群・包絡線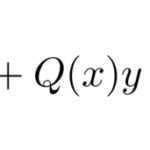
リカッチ(リカティ、Riccati)の微分方程式は の形をしている。一般的には解けないが、 1つの特解 がわかっているときは とおくことでベルヌーイの微分方程式に帰着して解ける。ベルヌーイ型 …
もっと読む 【微分方程式】例題で学ぶ:リカッチ(リカティ)型の解法
ラプラス変換は微分方程式を解くための道具でしかない。ここでは、面倒な積分計算は書かずにイメージだけ伝えたい。ラプラス変換の応用の要点は 微分方程式・積分方程式を簡単に解くために遠回りする ということである。 解きたい方 …
もっと読む 【はじめに】ラプラス変換を使う意味をわかりやすく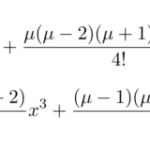
ルジャンドルの微分方程式 を解いて2つの特殊解を求める。微分方程式は まわりの級数展開により解いていく。「【微分方程式】級数解による解法(整級数)」の手法がそのまま使える。 得られる2つの …
もっと読む 【微分方程式】ルジャンドルの微分方程式/級数解による解法
一般解が以下の超幾何関数 で表すことができる超幾何微分方程式(ガウスの微分方程式) がある。この微分方程式は をもつため、「【微分方程式】確定特異点と級数の置き方 …
もっと読む 【微分方程式】超幾何微分方程式(ガウスの微分方程式) /一般解の導出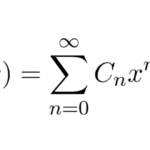
確定特異点のある微分方程式を級数解で解く。 ここでは特異点とは何かを説明し、解法をみていく。それを用いて後で例題を解いていく。 例題として、確定特異点のある微分方程式は以下のようなものである( が確定特異点)。 &nb …
もっと読む 【微分方程式】確定特異点と級数解の置き方/計算のコツ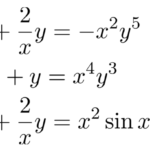
以下のベルヌーイ型と呼ばれる微分方程式(Bernoulli differential equation)の解法を説明する。 特徴は、左辺は線形型に見えるが右辺に が含まれることである。 こ …
もっと読む 【微分方程式】例題で学ぶ:ベルヌーイ型の解法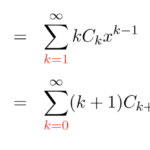
微分方程式を級数解によって解くとは、微分方程式の解の形を などと置いてしまって展開係数 を求める問題に替えて解くことである。例題を見ていこう。 例題 以下の微分方程式を級数を用いて解け。 & …
もっと読む 【微分方程式】例題で学ぶ:級数解による解法(整級数)