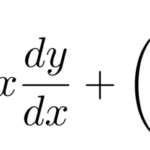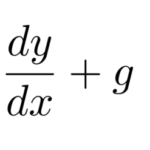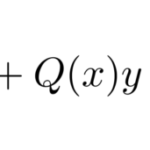微分方程式の同次型は
![]()
の形をとる。このタイプの微分方程式の解き方を例題を通して学習する。
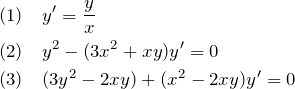
1. 同次型の微分方程式
同次型とは?
「同次」というのは次数が同じという意味である。 例として
![]()
のような形をしている場合である。 このとき、カッコの中身はすべて2次式であり、すべて同じ次数を取っている。
左辺を移項して、![]() の形にしてやると
の形にしてやると
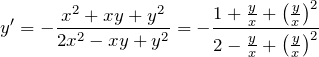
となる。すべて同じ次数であるため、![]() で割ったときに
で割ったときに ![]() の形が現れることが特徴である。
の形が現れることが特徴である。
同次型を見分ける眼を養う
同次型がどれか見分けられないと、解法を覚えても仕方ない。 ここでは、同次型を見分ける眼を養うために微分方程式を3つ用意した。 このうち一つは同次型ではない。
同次型ではないのはどの微分方程式だろうか。
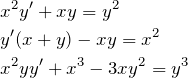
![]() の形にしなくても見分けがつくだろうか。
正解はもちろん、2番目の式である。
の形にしなくても見分けがつくだろうか。
正解はもちろん、2番目の式である。
![]() の係数は1次だが、それ以外の項では2次になっているためである。
の係数は1次だが、それ以外の項では2次になっているためである。
このように、適切に微分方程式のタイプを見分けることができないと 解法を覚えていても役に立たないので注意する。
同次型の解法
同次型の一般的な形が
![]()
となることは先に述べた。
この微分方程式は「変数を変換する」ことで解ける。
![]() とおくと、
とおくと、
![]()
である(![]() も
も![]() の関数であることに注意する)。
これを(*)へ代入して、
の関数であることに注意する)。
これを(*)へ代入して、
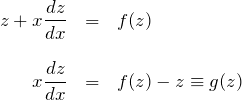
新たに得たこの微分方程式は、変数 ![]() と
と ![]() がバラバラにわかれた「変数分離型」である。 したがって、「変数分離型の解法」を使うことができる。
がバラバラにわかれた「変数分離型」である。 したがって、「変数分離型の解法」を使うことができる。
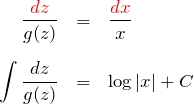
最終的な解は ![]() と
と ![]() で表されるため、
で表されるため、
![]() によって
によって ![]() と
と ![]() の式に戻せばよい。
の式に戻せばよい。
具体的な問題の解き方は例題を使っておこなう。その前に、上の解答の流れをまとめておこう。
同次型微分方程式の解法まとめ
同次型の解き方の流れをまとめておく。
-
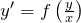 の形をつくる
の形をつくる 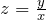 とおき、
とおき、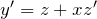 を元の式に代入
を元の式に代入- 「変数分離型」に帰着するため、変数分離型を解く
 と
と 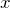 の式を
の式を 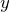 と
と 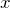 の式に直す
の式に直す
2. 例題の解答
以下の解答の ![]() は定数である。
は定数である。
例題(1)の解答
![]()
に対して、![]() とおくと、
とおくと、
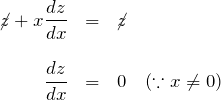
したがって、
![]()
* この単純な例題は変数分離型でも解ける。
例題(2)の解答
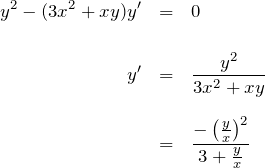
![]() に変換:
に変換:
![]()
元の微分方程式を ![]() で表す:
で表す:
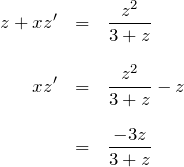
変数分離型の解法:
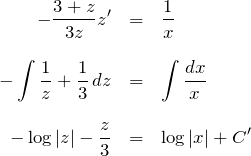
![]() を使い、
を使い、 ![]() の式にする:
の式にする:
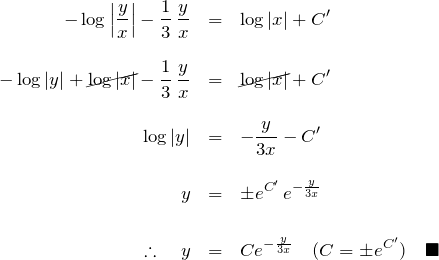
例題(3)の解答
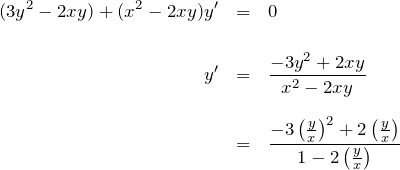
![]() に変換:
に変換:
![]()
元の微分方程式に代入して整理:
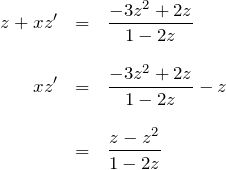
変数分離型の解法:
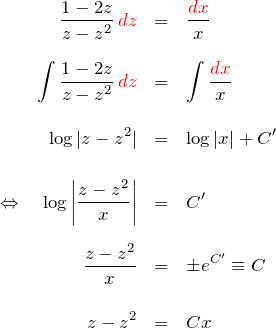
![]() を
を ![]() に直す:
に直す:
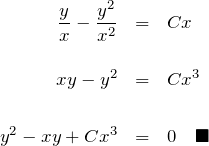
* 無理に ![]() の形にして答えなくてもよいです。
の形にして答えなくてもよいです。
3. まとめ
ここでは同次型の微分方程式の解法を扱った。 ![]() として「変数分離型」に帰着することを学んだ。 ここで見てきたように、変数変換により微分方程式の形が見慣れた形になることがよくある。
として「変数分離型」に帰着することを学んだ。 ここで見てきたように、変数変換により微分方程式の形が見慣れた形になることがよくある。
問題によっては、「こう置いてくれたら解ける」と訴えかけてくる問題もあるため、 変数変換によって微分方程式を解くという発想は常に持っておこう。