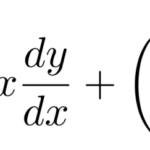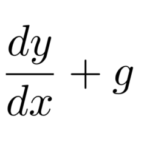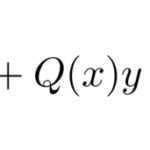ここでは、「変数分離形」の微分方程式を例題を使って学習する。いろいろな微分方程式がこのタイプに帰着することがあるので、解けるようにしておきたい。
次の変数分離形の微分方程式を解いて、一般解を求めよ。
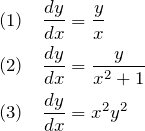
1. 変数分離形
よく出てくるタイプなので絶対におさえておくこと。
変数分離形とは何か
変数分離形は下のようなタイプで、![]() と
と ![]() を分離できる。
を分離できる。
![]()
この微分方程式の右辺は見ての通り、 ![]() のかたまりと
のかたまりと ![]() のかたまりに分けることができる。
のかたまりに分けることができる。
例:
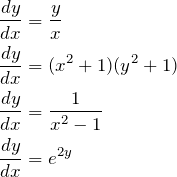
![]() が定数の場合もある。
が定数の場合もある。
したがって、
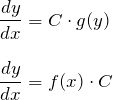
もまた変数分離形の仲間であり、ここで学ぶ解法が使える。
変数分離形の解き方
あたかも ![]() が項であるかのように、 与えられた式を変形しよう。
が項であるかのように、 与えられた式を変形しよう。
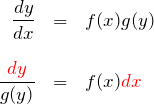
両辺に積分記号をつける。
![]()
これが変数分離形の解き方である。
![]() に関する式は左辺に、
に関する式は左辺に、![]() に関する式は右辺に集めれば良い。そのあと両辺を積分して解を求める。
に関する式は右辺に集めれば良い。そのあと両辺を積分して解を求める。
式変形では、あたかも ![]() が項であるかのように扱う。
が項であるかのように扱う。
* ![]() を一つの項として扱うのであれば、
を一つの項として扱うのであれば、
![]()
と変形して、両辺を ![]() で積分すれば、
で積分すれば、
![]()
となり、
![]()
に一致する。
2. 例題の解答
ここではあたかも ![]() を独立な項であるかのように書いて解答する。
を独立な項であるかのように書いて解答する。
例題(1)の解答
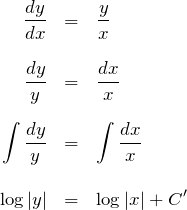
ここで絶対値に注意する。また、不定積分の ![]() を忘れない。
を忘れない。
![]() を外す。
を外す。
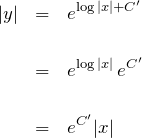
絶対値を外す。
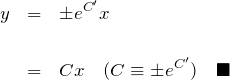
* 最後の行で定数 ![]() を
を ![]() を用いて置いた。 ここで
を用いて置いた。 ここで ![]() は0を含めたすべての実数をとる。 というのも
は0を含めたすべての実数をとる。 というのも ![]() に対応する
に対応する ![]() は元々の微分方程式の解になっているからである。
は元々の微分方程式の解になっているからである。
例題(2)の解答
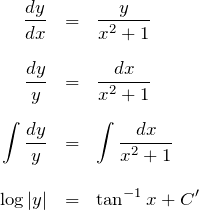
![]() をとって、絶対値を外す:
をとって、絶対値を外す:
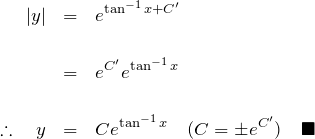
* ![]() は
は ![]() を含むすべての実数である。
を含むすべての実数である。![]() に対応する
に対応する ![]() はもともとの微分方程式の解になっている。
はもともとの微分方程式の解になっている。
例題(3)の解答
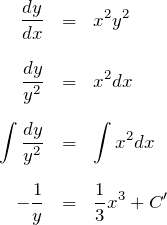
![]() はすべての実数。
はすべての実数。
![]() の形に直しておく。
の形に直しておく。
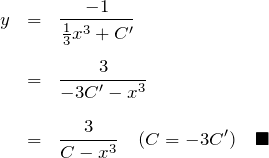
* 得られた ![]() を微分してチェックすることは計算ミスを防ぐ上で重要である。
を微分してチェックすることは計算ミスを防ぐ上で重要である。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{d}{dx}\left[\frac{3}{C-x^3}\right] &=&\frac{9x^2}{(C-x^3)^2}\\\\ &=&x^2 \left(\frac{3}{C-x^3}\right)^2\\\\ &=&x^2 y^2 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-bc1c21f5c22799ad23d33b873c3b5a3e_l3.png)
確かに、微分方程式を満たす。
3. まとめ
変数分離形の解法は、最も基本的な微分方程式の解き方のひとつである。 より難しい微分方程式も、変数分離形に帰着させて解くといったことが頻繁にあるため、 変数分離形はマストで解けるようにしておかなければならない。