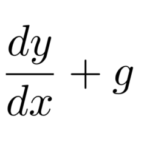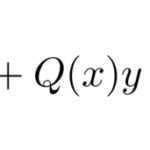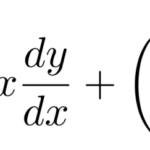ここでは以下のような微分方程式を解いていく。
![]()
このタイプは、![]() の変数変換により変数分離型に帰着する。 以下では例題を通して、このタイプの微分方程式を解いていこう。
の変数変換により変数分離型に帰着する。 以下では例題を通して、このタイプの微分方程式を解いていこう。
例題
![]()
1. 一般的な解き方
変数変換により変数分離型に帰着することを確認する。 最後に解法の流れをまとめた。
変数変換
![]()
について、
![]()
と変数変換する。両辺を ![]() で微分して、
で微分して、
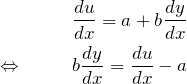
となる。微分方程式(*)の両辺に ![]() をかけて
をかけて
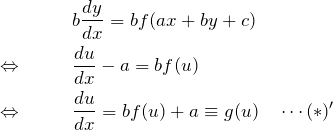
となる。
変数分離型に帰着
上で得られた、新たな ![]() に関する微分方程式(*)’は変数分離型である。 つまり、
に関する微分方程式(*)’は変数分離型である。 つまり、
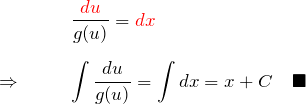
として解くことができる(![]() )。
)。
解法のまとめ
以上をまとめておく。
ポイント
について
![]()
について
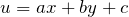 とおく(
とおく(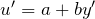 )
)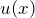 に関する微分方程式は変数分離型となる
に関する微分方程式は変数分離型となる- 変数分離型を解いて、解を求める
-
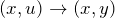 に戻す
に戻す
2. 例題の解答
以下の解答で、![]() などは定数である。
などは定数である。
例題(1)の解答
![]()
変数変換:
![]()
変数分離型に帰着・変数分離型を解く:
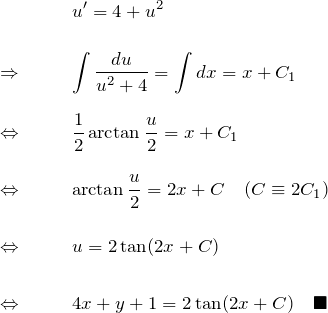
例題(2)の解答
![]()
![]() は解ではない(
は解ではない(![]() )ため、
)ため、
![]()
を考える。
変数変換:
![]()
変数分離型に帰着:
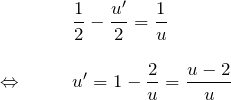
ここで、![]() は解である(
は解である(![]() )。 つまり、
)。 つまり、![]() は解である。
は解である。
![]() のとき、変数分離型を解く:
のとき、変数分離型を解く:
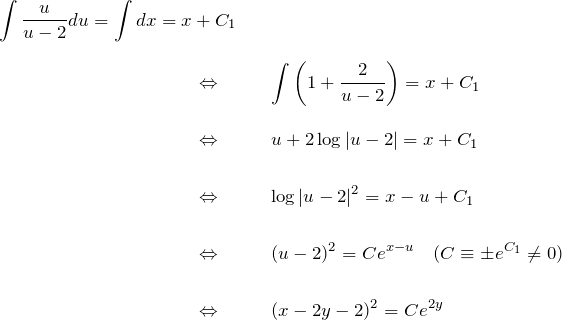
答え:
![]() をまとめておく。
をまとめておく。
![]()
ただし、![]() は
は ![]() を含む定数。
を含む定数。
*答え方は、![]() をまとめない形でも良い。
をまとめない形でも良い。
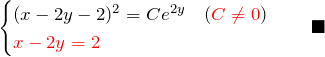
3. まとめ
![]() で変数変換すれば変数分離型に帰着して容易に解けることがわかった。 このタイプでは変数変換の仕方がわかりやすいので簡単だと思う。しかし、
で変数変換すれば変数分離型に帰着して容易に解けることがわかった。 このタイプでは変数変換の仕方がわかりやすいので簡単だと思う。しかし、![]() で置くということは覚えておかなくてはならない。
で置くということは覚えておかなくてはならない。