【結晶中の原子の磁性】軌道角運動量の消失/ヤーン・テラー効果
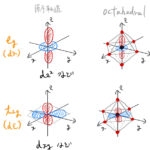
結晶中の原子の磁性として、軌道角運動量の消失(凍結)とヤーン・テラー(Jahn-Teller)効果について述べておく。 原子の磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3 …
もっと読む 【結晶中の原子の磁性】軌道角運動量の消失/ヤーン・テラー効果バター猫のパラドックス

結晶中の原子の磁性として、軌道角運動量の消失(凍結)とヤーン・テラー(Jahn-Teller)効果について述べておく。 原子の磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3 …
もっと読む 【結晶中の原子の磁性】軌道角運動量の消失/ヤーン・テラー効果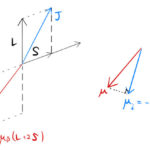
ここでは孤立した多電子原子の磁性を考える。結晶中にある原子の磁性との違いを理解しておきたい。 原子の磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3つである。 1電子原子の磁 …
もっと読む 【多電子原子の磁性】全角運動量/ランデg因子/フント則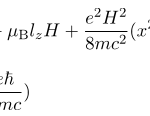
ここでは孤立した1電子原子の磁性を考える。 磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3つである。 1電子原子の磁性(孤立)← 多電子原子の磁性(孤立) 結晶中の原子の磁 …
もっと読む 【1電子原子の磁性】ハミルトニアン(軌道角運動量)/反磁性モーメント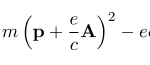
ローレンツ力(Lorentz force)から以下のハミルトニアンを導出することができる。逆に辿れば、ハミルトニアンからローレンツ力を導くこともできる。難しいのは、ローレンツ力が働く電子の運動方程式が導かれるようなラグ …
もっと読む ローレンツ力 → 1電子原子のハミルトニアン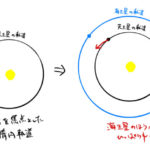
時間に依存しない摂動論(縮退なし)の概要とエネルギー計算を説明する。2次摂動までのエネルギーと波動関数は以下の通り。1次までで良い時は、2次摂動(赤色)は無視して計算すれば良い。(2次摂動の計算はそこそこ大変) ポイン …
もっと読む 摂動とは/摂動エネルギーと状態の計算(1次・2次)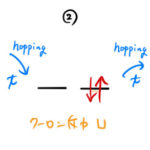
直接交換相互作用とは、隣接する原子の軌道にある2つの電子に働く相互作用である。ここでは、2つの原子間の電子のホッピングによる相互作用を考える。(運動交換ともいう。) ハイゼンベルグ相互作用 の項では、2つの電子はそれぞ …
もっと読む 直接交換相互作用(電子のホッピング)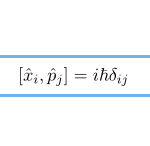
位置演算子 と運動量演算子 の交換関係を調べる。結果は下の通り。 はクロネッカーのデルタである( のときのみ 1 になる)。 x,pの交換関係 一次元の の交換関係は として以下の計算を見 …
もっと読む 位置演算子と運動量演算子の交換関係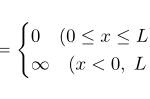
1次元井戸型ポテンシャルのシュレディンガー方程式を解いていく。得られた結果から、最後は不確定性原理に少し触れる。 自由電子模型:無限に広い場合(3次元) 自由電子模型:端がない周期的な系(1次元、3次元) 1次元井戸型 …
もっと読む 1次元井戸型ポテンシャル(無限大)と不確定性関係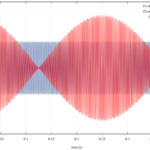
強制振動とは、ブランコに乗っている人を後ろから押してやるみたいに、振動数 で自由振動している系を外場 によって強制的に振動させる運動のことである。もともとの に近い振動数で外場 を与えたときには「うなり」が発生する。以 …
もっと読む 【振動】「うなり」と強制振動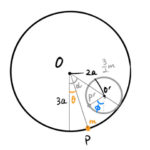
微小振動の例として円筒振り子がある。この円筒振り子の中にさらに円柱を入れて2つの微小振動を見る。以下の例題で考える。 左が厚みのない円筒の振り子。右が円筒振り子内の円柱(灰色)。 半径 の円筒振り子の軸まわりの慣性モ …
もっと読む 【振動】円筒振り子の中の円柱(微小振動)