結晶中の原子の磁性として、軌道角運動量の消失(凍結)とヤーン・テラー(Jahn-Teller)効果について述べておく。
原子の磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3つである。
- 1電子原子の磁性(孤立)
- 多電子原子の磁性(孤立)
- 結晶中の原子の磁性(集団)←
1. 軌道角運動量の消失(凍結)
ざっくりと、
- 結晶中を電子が動き回る
- 中心対称ポテンシャルではない
- 軌道角運動量は平均して0(軌道角運動量の消失)
のようになる。以下ではこれを説明する。
1. 結晶中にある原子の磁性は孤立原子の磁性とは違ったものとなる。とくに、
2. スピン軌道相互作用がなければ、孤立原子にある電子の全軌道角運動量 ![]() は運動の定数(保存量)であった。しかし、結晶中を動き回る電子においては、もはや原子を中心とした中心対称ポテンシャルではない。
は運動の定数(保存量)であった。しかし、結晶中を動き回る電子においては、もはや原子を中心とした中心対称ポテンシャルではない。
3. 結晶中のポテンシャルを受ける電子の軌道角運動量は保存しない。この場合、軌道角運動量は死んでいる(軌道角運動量の消失(凍結))。
3について少し説明する。
![]() の期待値
の期待値 ![]() を考える。
を考える。![]() は
は
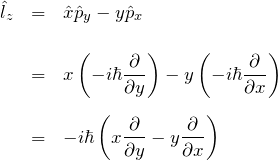
であり、期待値は
![]()
である。![]() の意味はある波動関数に対して期待をとるという意味である。ここで、外磁場がない場合は結晶中の波動関数を実関数でとることができる。その結果、上の式の
の意味はある波動関数に対して期待をとるという意味である。ここで、外磁場がない場合は結晶中の波動関数を実関数でとることができる。その結果、上の式の![]() の部分は実関数となる。
の部分は実関数となる。
![]() の前に
の前に ![]() があるため、
があるため、![]() は純虚数となり、観測可能量(オブザーバブル)としてはゼロ以外にない。これを、
は純虚数となり、観測可能量(オブザーバブル)としてはゼロ以外にない。これを、
![]()
として軌道角運動量の消失と呼ぶ。
以上の軌道角運動量の消失は、![]() 電子系において顕著であり、
電子系において顕著であり、![]() 電子系の場合には軌道角運動量は残る。それは、
電子系の場合には軌道角運動量は残る。それは、![]() 電子が結晶を動き回る遍歴性をもつ一方で、
電子が結晶を動き回る遍歴性をもつ一方で、![]() 電子は原子に局在しているために孤立原子と同じような状況になっているためである。
電子は原子に局在しているために孤立原子と同じような状況になっているためである。
したがって、遍歴電子を持つ ![]() 遷移金属については軌道角運動量の消失
遷移金属については軌道角運動量の消失 ![]() により、全角運動量の値は
により、全角運動量の値は ![]() として全スピン角運動量で置き換えても良い。
として全スピン角運動量で置き換えても良い。
一方で、局在電子を持つ ![]() 希土類については軌道角運動量は消失しにくいため、全角運動量は
希土類については軌道角運動量は消失しにくいため、全角運動量は ![]() のままである。
のままである。![]() はフント則(ルール3)によって、半閉殻以下(電子数7以下)であれば
はフント則(ルール3)によって、半閉殻以下(電子数7以下)であれば ![]() であり、半閉殻以上(電子数7以上)であれば
であり、半閉殻以上(電子数7以上)であれば ![]() であった。
であった。
2. 結晶場/Jahn-Teller効果
2.1 3d軌道(原子軌道)とt2g、eg軌道
![]() 原子軌道は以下の5つの形をとる。
原子軌道は以下の5つの形をとる。
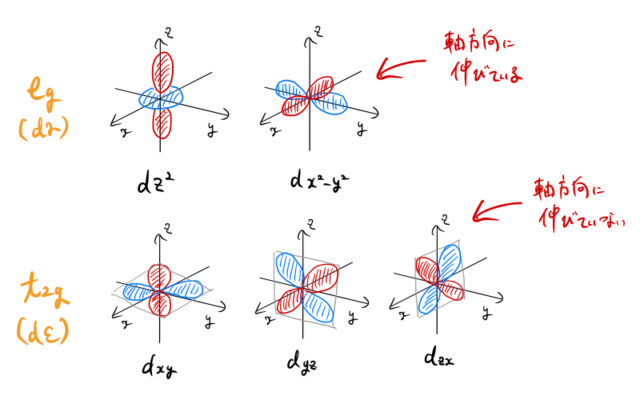
ここで、5つの軌道を対称性から、2つの ![]() と 3つの
と 3つの ![]() に分ける。結晶場の理論で大事なことは、
に分ける。結晶場の理論で大事なことは、
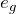 軌道は軸方向に伸びている(電子の存在確率が大きい)
軌道は軸方向に伸びている(電子の存在確率が大きい)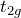 軌道は軸方向に伸びていない
軌道は軸方向に伸びていない
ということである。孤立原子の状態であれば、これらの5つの軌道は縮退して、同一のエネルギー状態をとる。
結晶中の ![]() 軌道のエネルギーを考える。例として、陽イオン Cu
軌道のエネルギーを考える。例として、陽イオン Cu![]() が6個の陰イオンに囲まれた八面体(Octahedral)を考える。このとき、下図に示すようにエネルギー準位の縮退は解ける。
が6個の陰イオンに囲まれた八面体(Octahedral)を考える。このとき、下図に示すようにエネルギー準位の縮退は解ける。
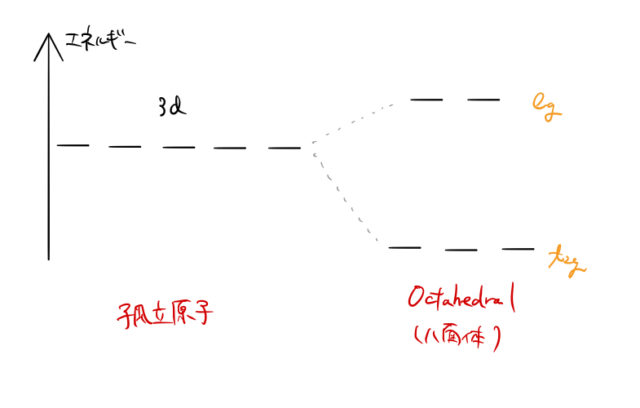
この理由を考える。下図に ![]() と
と ![]() の場合の様子を描いた。Octahedralに囲まれている場合、赤色で示した陰イオンはすべて軸上に存在する。したがって、陰イオンの内核電子の存在確率は軸の上で大きい。
の場合の様子を描いた。Octahedralに囲まれている場合、赤色で示した陰イオンはすべて軸上に存在する。したがって、陰イオンの内核電子の存在確率は軸の上で大きい。
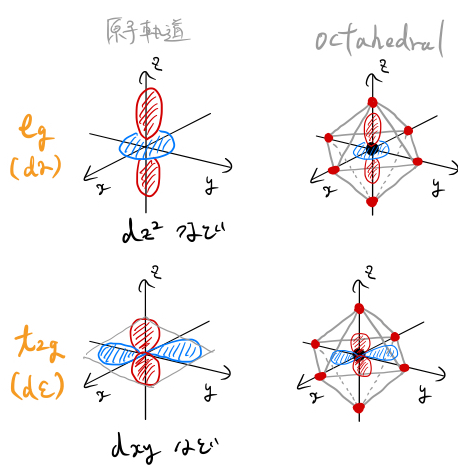
![]() の電子軌道は軸方向に伸びているため、電子の存在確率は軸方向で大きい。したがって、
の電子軌道は軸方向に伸びているため、電子の存在確率は軸方向で大きい。したがって、![]() の電子と陰イオンの電子のクーロン斥力によりエネルギーは大きくなる
の電子と陰イオンの電子のクーロン斥力によりエネルギーは大きくなる![]() 。
。
一方で、![]() の電子軌道は軸方向に伸びていないため、電子の存在確率は軸方向で小さい。したがって、
の電子軌道は軸方向に伸びていないため、電子の存在確率は軸方向で小さい。したがって、![]() の電子と陰イオンの電子のクーロン斥力によりエネルギーは
の電子と陰イオンの電子のクーロン斥力によりエネルギーは ![]() に比べて小さくなる。
に比べて小さくなる。
以上のように、八面体の場合(NaCl型構造やペロブスカイト型構造など)では ![]() のエネルギーは
のエネルギーは ![]() のエネルギーより大きくなる。また、四面体の場合は逆に、
のエネルギーより大きくなる。また、四面体の場合は逆に、![]() のエネルギーが
のエネルギーが ![]() のエネルギーより大きくなる。
のエネルギーより大きくなる。
2.2 Jahn-Teller効果
再度、例としてOctahedralに陰イオンに囲まれた陽イオンの Cu![]() を考える。フント則に従ってスピン配置を決めると下図(左)のようになる。
を考える。フント則に従ってスピン配置を決めると下図(左)のようになる。![]() である。
である。
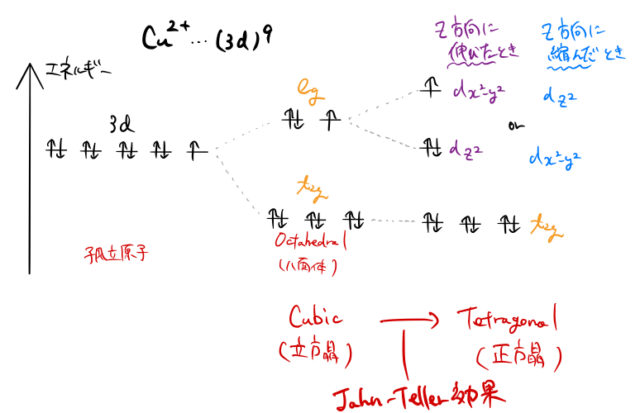
図(中)に、Octahedralの場合の電子配置を描いた。ここで、2つの![]() 軌道に3つの電子が配置されている。図(右)には 立方晶が
軌道に3つの電子が配置されている。図(右)には 立方晶が ![]() 方向に伸びた場合と縮んだ場合の
方向に伸びた場合と縮んだ場合の ![]() のエネルギー準位を表している。このように自発的に歪みが発生することをヤーン・テラー効果という。以下では歪みが発生する理由を説明する。
のエネルギー準位を表している。このように自発的に歪みが発生することをヤーン・テラー効果という。以下では歪みが発生する理由を説明する。
立方晶を![]() 方向に伸ばして正方晶にしたとする。このとき、2つの
方向に伸ばして正方晶にしたとする。このとき、2つの![]() 軌道は下図のようになる。
軌道は下図のようになる。
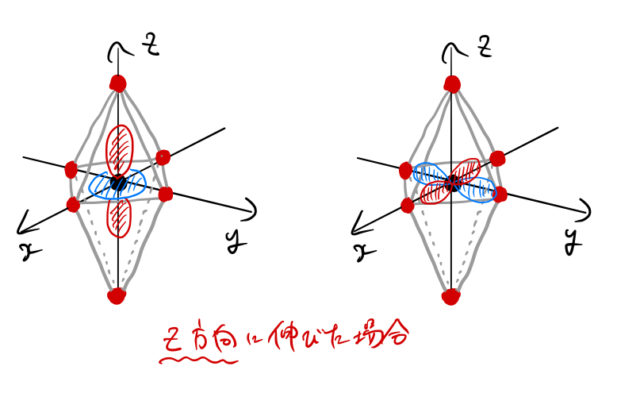
左の![]() 軌道の電子の存在確率は
軌道の電子の存在確率は ![]() 軸方向で大きいが、正方晶になったため
軸方向で大きいが、正方晶になったため ![]() 軸上の陰イオンの電子とのクーロン斥力は小さくなる。
軸上の陰イオンの電子とのクーロン斥力は小さくなる。
一方で、右の![]() については、電子の存在確率は
については、電子の存在確率は ![]() 軸方向で大きい。
軸方向で大きい。![]() 方向に伸ばした場合は
方向に伸ばした場合は ![]() 方向に縮むため、陰イオンの電子と
方向に縮むため、陰イオンの電子と ![]() の電子とのクーロン斥力は大きくなる。
の電子とのクーロン斥力は大きくなる。
したがって、![]() 軸方向に伸びた正方晶では
軸方向に伸びた正方晶では ![]() のエネルギーは
のエネルギーは![]() のエネルギーより小さくなる。逆に
のエネルギーより小さくなる。逆に ![]() 方向に縮んだ場合は
方向に縮んだ場合は ![]() のエネルギーは
のエネルギーは![]() のエネルギーより大きくなる。
のエネルギーより大きくなる。
このような歪みが必ず起こるわけではない。ヤーン・テラー歪みにより、上記のような電子系においてエネルギーは得するが、格子系において歪みエネルギーの分だけエネルギーは損することになる。ヤーン・テラー効果により自発的な歪みが起こるためには電子系のエネルギー減少分が歪みエネルギーより大きい必要がある。
ここでは Cu![]() を例にとったが、Ni
を例にとったが、Ni![]() はどうだろうか。この場合、
はどうだろうか。この場合、![]() である。電子配置として
である。電子配置として ![]() に6個の電子が入り、
に6個の電子が入り、![]() に2個の電子が入った状態を考える。
に2個の電子が入った状態を考える。
![]() と
と ![]() にそれぞれ電子が1個ずつ存在するため、正方晶に歪んだ場合でも電子系のエネルギー利得はない。したがって、Ni
にそれぞれ電子が1個ずつ存在するため、正方晶に歪んだ場合でも電子系のエネルギー利得はない。したがって、Ni![]() などの
などの ![]() の場合はヤーン・テラー効果は起こらない
の場合はヤーン・テラー効果は起こらない![]() 。ヤーンテラー効果が見られるのは
。ヤーンテラー効果が見られるのは ![]() や
や ![]() などである。
などである。
3. まとめ
結晶中の原子の磁性として、軌道角運動量の消失とヤーン・テラー効果について説明した。ここで扱ったヤーン・テラー効果は静的ヤーン・テラー効果と呼ばれるものである。もっと複雑な系では複雑なヤーン・テラーが存在する。
![]() :
:![]() 原子軌道は球面調和関数などを用いて表すことができるため具体的に斥力エネルギーを計算することも可能である。
原子軌道は球面調和関数などを用いて表すことができるため具体的に斥力エネルギーを計算することも可能である。
![]() :これには諸説ある。ここではd8の状態についてヤーンテラー効果は起こらないとした。
:これには諸説ある。ここではd8の状態についてヤーンテラー効果は起こらないとした。