ここでは孤立した1電子原子の磁性を考える。
磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3つである。
- 1電子原子の磁性(孤立)←
- 多電子原子の磁性(孤立)
- 結晶中の原子の磁性(集団)
ここでは1番目の場合を考える。![]() 方向に磁場
方向に磁場 ![]() があるとき、 1電子原子のハミルトニアンは以下のようになる(ここではスピンは考えない)。
があるとき、 1電子原子のハミルトニアンは以下のようになる(ここではスピンは考えない)。
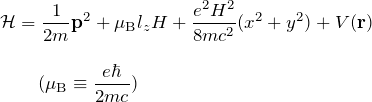
1. ハミルトニアンを求める
上のハミルトニアンをつくる。
1.1 ベクトルポテンシャル
まず、時間に依存しない定磁場 ![]() が
が ![]() 方向にあるとき、
方向にあるとき、
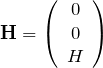
である。![]() を満たすベクトルポテンシャル
を満たすベクトルポテンシャル ![]() のひとつは
のひとつは
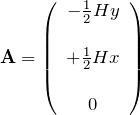
で与えられる。
1.2 ハミルトニアン
一般的な 1電子原子のハミルトニアンは、
![]()
である。ここで、![]() は1個の電子が受ける原子からのポテンシャルを表す。ここでは軌道角運動量のみを考え、スピンを考えない。したがってスピン軌道相互作用もゼーマン項もハミルトニアンには現れない。
は1個の電子が受ける原子からのポテンシャルを表す。ここでは軌道角運動量のみを考え、スピンを考えない。したがってスピン軌道相互作用もゼーマン項もハミルトニアンには現れない。
これを展開して、
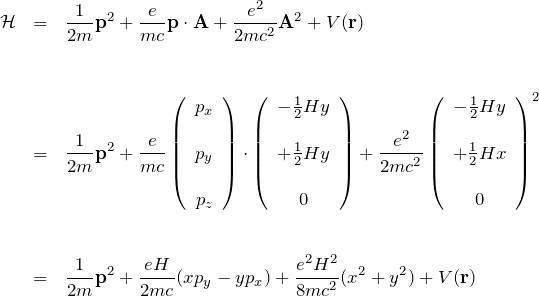
第二項について角運動量 ![]() と、ボーア磁子
と、ボーア磁子 ![]() を用いて、
を用いて、
![]()
この結果から任意の方向にある磁場 ![]() に対しては、第二項は
に対しては、第二項は
![]()
となると考えられる。
これは、角運動量 ![]() に磁気モーメント
に磁気モーメント ![]() が付随していることを表す。中心対称の
が付随していることを表す。中心対称の ![]() に対しては角運動量は定数となる。したがって、
に対しては角運動量は定数となる。したがって、![]() の固有値は
の固有値は ![]() 、
、![]() の固有値は
の固有値は ![]() となる。この結果はスピン軌道相互作用がない、かつ原子が孤立している場合の話である。
となる。この結果はスピン軌道相互作用がない、かつ原子が孤立している場合の話である。
多電子系の原子(孤立)の場合:1電子の角運動量 ![]() は保存量ではない。この場合は全角運動量
は保存量ではない。この場合は全角運動量 ![]() が保存量となる(スピン軌道相互作用がない場合)。スピン軌道相互作用があれば全角運動量
が保存量となる(スピン軌道相互作用がない場合)。スピン軌道相互作用があれば全角運動量 ![]() が保存量になる。
が保存量になる。
結晶中の原子(集団)
の場合:中心対称のポテンシャル ![]() ではないため、軌道角運動量
ではないため、軌道角運動量 ![]() も全軌道角運動量
も全軌道角運動量 ![]() も保存しない(一定ではない)。例えば、
も保存しない(一定ではない)。例えば、![]() 電子をもった金属系(Fe,Co,Ni,…)などでは軌道角運動量は死んでいる(軌道角運動量の凍結)。
電子をもった金属系(Fe,Co,Ni,…)などでは軌道角運動量は死んでいる(軌道角運動量の凍結)。
2. 反磁性モーメント/反磁性帯磁率
まず、ハミルトニアンを外磁場で微分すると何がわかるか考える。
下に示す外磁場中の磁気モーメント(双極子モーメント)![]() の
エネルギーの形 から、ハミルトニアンも同様の形をとる。
の
エネルギーの形 から、ハミルトニアンも同様の形をとる。
![]()
これを磁場 ![]() で微分してみる
で微分してみる![]() 。
。
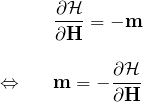
したがって、ハミルトニアン(あるいはエネルギー)を磁場 ![]() で微分して符号を変えたものは、磁気モーメントを表す。
で微分して符号を変えたものは、磁気モーメントを表す。
引き続き ![]() 方向に磁場
方向に磁場 ![]() がある場合を考える。1.2で得られたハミルトニアンの第三項を磁場
がある場合を考える。1.2で得られたハミルトニアンの第三項を磁場 ![]() で微分して符号を変える。
で微分して符号を変える。
![]()
得られた磁気モーメントは負であるため、反磁性モーメント(diamagnetic moment)と呼ぶ。もともとのハミルトニアンにはスピン角運動量を含んでいない。したがって、反磁性モーメントは軌道角運動量による項である。
電子の波動関数が球対称である場合を考える。このとき、位置の平均は
![]()
となる。したがって、反磁性モーメントの平均 ![]() は
は
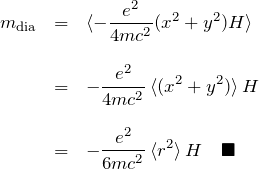
外磁場 ![]() によって上の値に対応する反磁性モーメントが誘起されたと考えると、反磁性帯磁率(diamagnetic susceptibility)は
によって上の値に対応する反磁性モーメントが誘起されたと考えると、反磁性帯磁率(diamagnetic susceptibility)は
![]()
多電子系の閉殻電子系などの場合でも同様の式が反磁性帯磁率をもつ。この場合は、電子の個数分だけ上の反磁性モーメントが誘起されるため、反磁性帯磁率は電子数倍すればよい。
![]()
3. まとめ
1電子原子のハミルトニアンを求めた。反磁性モーメントや反磁性帯磁率のについても求めた。ここでは、1電子の軌道角運動量 ![]() しか考えていない。さらなる議論のためには、このハミルトニアンにスピン角運動量によるハミルトニアンを加える必要がある。
しか考えていない。さらなる議論のためには、このハミルトニアンにスピン角運動量によるハミルトニアンを加える必要がある。
![]() :ベクトルの微分はベクトルを表す。わかりにくい場合は成分ごとに微分していると思えば良い。
:ベクトルの微分はベクトルを表す。わかりにくい場合は成分ごとに微分していると思えば良い。