位置演算子と運動量演算子の交換関係【計算】

　位置演算子 $\hat{\bf x}$ と運動量演算子 $\hat{\bf p}$ の交換関係を調べる。結果は下の通り。 $\delta_{ij}$ はクロネッカーのデルタである（ $i=j$ のときのみ 1 になる）。

x,pの交換関係

$\begin{eqnarray*} [\hat{x}_i,\hat{p}_j]=i\hbar \delta_{ij} \end{eqnarray*}$

　一次元の $\hat{x},\hat{p}_x$ の交換関係は $i=j$ として以下の計算を見ていけば良い。

交換関係
xとpの交換関係
まとめ

交換関係

　量子力学の中では、２つの演算子 $\hat{A},\hat{B}$ は一般に交換しない。つまり、

$\begin{eqnarray*} \hat{A}\hat{B}\neq \hat{B}\hat{A} \end{eqnarray*}$

である。交換関係を表す記号として、

$\begin{eqnarray*} [\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A} \end{eqnarray*}$

が使われる。これは解析力学でのポアッソン括弧に対応する。

xとpの交換関係

$\hat{x}_i,\hat{p}_j, \;(i,j=x,y,z)$ の交換関係を調べる。

ポイント

演算子の交換関係の計算は具体的な関数を用意してやると見通しが良くなる。関数を用意しないと間違えやすい。

運動量演算子 $\hat{p}_j$ を ${\bf x}$ で表示 $^*$ ：

$\begin{eqnarray*} \hat{p}_j=-i\hbar \frac{\partial}{\partial j} \quad(j=x,y,z) \end{eqnarray*}$

位置演算子 $\hat{\bf x}$ を ${\bf x}$ で表示 $^*$ ：

$\begin{eqnarray*} \hat{x}=x \end{eqnarray*}$

交換関係を求める：

　適当な関数 $\phi(x,y,z)$ を用いる。 $i=j$ と $i\neq j$ の場合について計算する。

$i=j=x$ の場合：

$\begin{eqnarray*} [\hat{x},\hat{p}_x]\phi(x,y,z) &=& [\hat{x}\hat{p}_x-\hat{p}_x\hat{x}]\phi(x,y,z)\\\\ &=& \left[x\left(-i\hbar \frac{\partial}{\partial x}\right)-\left(-i\hbar \frac{\partial}{\partial x}\right)x\right]\phi(x,y,z)\\\\ &=& -i\hbar\left[ x\frac{\partial}{\partial x} \phi(x,y,z)- \frac{\partial}{\partial x}\textcolor{red}{\left(x \phi(x,y,z)\right)} \right]\\\\ &=& -i\hbar\left[ \cancel{x\frac{\partial}{\partial x} \phi(x,y,z)} - \textcolor{red}{\left(\phi(x,y,z)+\cancel{x\frac{\partial}{\partial x}\phi(x,y,z)}\right)} \right]\\\\ &=& i\hbar \phi(x,y,z) \end{eqnarray*}$

したがって、両辺の $\phi(x,y,z)$ の係数を比べて、

$\begin{eqnarray*} [\hat{x},\hat{p}]=i\hbar\quad \blacksquare \end{eqnarray*}$

　赤色で強調した部分は間違えやすい部分である。 $\phi(x,y,z)$ に $\textcolor{red}{x}$ をかけてから $x$ で偏微分するために、合成関数の微分の形になる。

$i\neq j$ の場合（例： $i=x,j=y$ ）：

$\begin{eqnarray*} [\hat{x},\hat{p}_y]\phi(x,y,z) &=& [\hat{x}\hat{p}_y-\hat{p}_y\hat{x}]\phi(x,y,z)\\\\ &=& \left[x\left(-i\hbar \frac{\partial}{\partial y}\right)-\left(-i\hbar \frac{\partial}{\partial y}\right)x\right]\phi(x,y,z)\\\\ &=& -i\hbar\left[ x\frac{\partial}{\partial y} \phi(x,y,z)- \frac{\partial}{\partial y}\textcolor{red}{\left(x \phi(x,y,z)\right)} \right]\\\\ &=& -i\hbar\left[ \cancel{x\frac{\partial}{\partial y} \phi(x,y,z)} - \textcolor{red}{\cancel{x\frac{\partial}{\partial y}\phi(x,y,z)}} \right]\\\\ &=&0\cdot\phi(x,y,z) \end{eqnarray*}$

したがって、両辺の $\phi(x,y,z)$ の係数を比べて、

$\begin{eqnarray*} [\hat{x},\hat{p}_y]=0\quad\blacksquare \end{eqnarray*}$

$i\neq j$ のときは、 $\phi(x,y,z)$ に $\textcolor{red}{y}$ をかけてから $x$ で偏微分するために、単に $x\partial\phi(x,y,z)/\partial y$ になる。

$x,p_z$ などの交換関係も同様に計算される。したがって、

x,pの交換関係

$\begin{eqnarray*} [\hat{x}_i,\hat{p}_j]=i\hbar \delta_{ij} \end{eqnarray*}$

クロネッカーのデルタ $\delta_{ij}$ は以下である。

$\begin{eqnarray*} \delta_{ij}=\begin{cases} 1\quad(i=j)\\ 0\quad(i\neq j) \end{cases} \end{eqnarray*}$

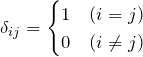
　最後の結果、位置と運動量の交換関係が 0 でないことがわかった。したがって、同時固有状態はとれない。これは、正確な位置と正確な運動量を同時に決定できないという不確定性原理と対応する。

参考：「同時固有状態を持つ」⇄「交換関係=0」

まとめ

　交換関係の計算のポイントは以下である。

適当な関数に作用させてみる
合成関数の積の微分に注意する

これだけでほとんどの交換関係の計算は対応できるだろう。

$^*$ ：位置演算子 $\hat{\bf x}$ と運動量演算子 $\hat{\bf p}$ は運動量空間での表示も可能である。

位置演算子と運動量演算子の交換関係

交換関係

xとpの交換関係

まとめ

2件のコメント

コメントを残すコメントをキャンセル

交換関係

xとpの交換関係

まとめ

2件のコメント

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル