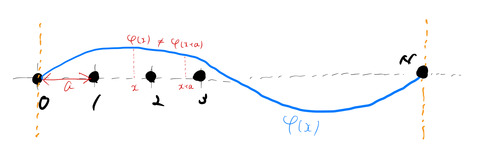
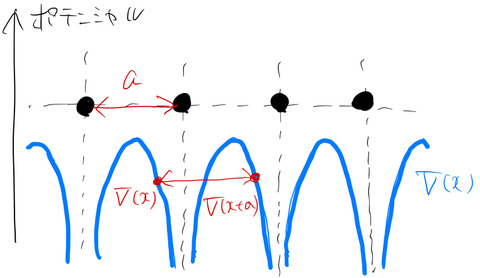
ブロッホの定理は、周期的に原子が並ぶ固体の波動関数に対して強力な道具となる。簡単のため1次元について説明する。周期的に格子間隔 ![]() で規則正しく原子が並んでいる場合、そのポテンシャル
で規則正しく原子が並んでいる場合、そのポテンシャル ![]() は図のように周期的になる。
は図のように周期的になる。
ブロッホの定理は ![]() の並進対称性から導かれる定理である。
の並進対称性から導かれる定理である。
- 自由電子模型:無限に広い場合(3次元)
- 自由電子模型:端がない周期的な系(1次元、3次元)
- 1次元井戸型ポテンシャル(無限井戸)
- 1次元井戸型ポテンシャル(有限井戸)
- 周期ポテンシャルのある場合(ブロッホの定理)←
- クローニッヒ・ペニー模型
1. ブロッホの定理を導く
1.1 並進させる
このとき、ある位置 ![]() から
から ![]() だけずれた点でもポテンシャルは同じ値になっている(ポテンシャルの並進対称性)。すなわち、
だけずれた点でもポテンシャルは同じ値になっている(ポテンシャルの並進対称性)。すなわち、
![]()
が成り立つ。 ![]() に並進させる演算子を
に並進させる演算子を![]() と定義すると、
と定義すると、
![]()
のように表すことができる。
波動関数![]() については一般に、
については一般に、
![]()
のように、格子![]() の並進に対する対称性はない。
の並進に対する対称性はない。
そこで、ポテンシャルが並進対称性をもつときの波動関数 ![]() を調べたい。
を調べたい。![]() は時間に依存しないシュレディンガー方程式、
は時間に依存しないシュレディンガー方程式、
![]()
であらわすことができる。
1.2 シュレディンガー方程式の並進対称性
![]() の形を作るため、シュレディンガー方程式の両辺に
の形を作るため、シュレディンガー方程式の両辺に ![]() を作用させる。左辺は、
を作用させる。左辺は、
![Rendered by QuickLaTeX.com \begin{eqnarray*}T_a[H(x)\varphi(x)]&=&H(x+a)\varphi(x+a)\\ \\&=&\left\{ T_a\left[-\frac{\hbar^2}{2m}p^2 \right] + T_a\left[V(x) \right]\right\} \varphi(x+a)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-474eb473f26c1e45ec48632c4d55505b_l3.png)
となる。ここで第2項の ![]() と同様に、第1項の運動エネルギーの項についても並進対称性をもつ(
と同様に、第1項の運動エネルギーの項についても並進対称性をもつ(![]() が並進対称性をもつことに由来)。したがって、ハミルトニアン
が並進対称性をもつことに由来)。したがって、ハミルトニアン ![]() も並進対称性をもつ。
も並進対称性をもつ。
![]()
以上より式(1)は、
![Rendered by QuickLaTeX.com \begin{eqnarray*}T_a[H(x)\varphi(x)]=H(x)\varphi(x+a)=E\varphi(x+a)\\ \\\leftrightarrow H(x)T_a[\varphi(x)] = E T_a[\varphi(x)]\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-07b75acc05df162ad814b502c7005970_l3.png)
のようになる。この式から、![]() と
と![]() が交換可能であり同時固有関数をもつことがわかる。実際に、この式を見れば、
が交換可能であり同時固有関数をもつことがわかる。実際に、この式を見れば、![]() に
に ![]() を作用させたものがハミルトニアン
を作用させたものがハミルトニアン ![]() の固有関数となっていることが確認できる。
の固有関数となっていることが確認できる。
「同時固有関数をもつ」とは同じ固有関数の形で、複数の演算子に対する固有値方程式が作られるということである。
今の場合、演算子は ![]() と
と ![]() である。
である。![]() に対する固有値方程式は明らかに、シュレディンガー方程式、
に対する固有値方程式は明らかに、シュレディンガー方程式、
![]()
である。
1.3 並進演算子に対する固有値
![]() に対する固有値方程式の固有値を
に対する固有値方程式の固有値を ![]() と表せば、
と表せば、
![]()
である。これを満たす固有値 ![]() と固有関数
と固有関数 ![]() はどのような形であろうか。試しに、ポテンシャルと同じ周期性を持った周期関数
はどのような形であろうか。試しに、ポテンシャルと同じ周期性を持った周期関数 ![]() を用いて
を用いて
![]()
とでも置いてみる。この関数に対して式(2)の ![]() は
は
![]()
であり、式(2)の右辺は、
![]()
である。したがって式(2)は、
![]()
と書ける。
1.4 ブロッホの定理を得た
今の計算過程で出てきた、式(4)がブロッホの定理(1次元)である。すなわち、
![]()
がブロッホの定理である。あるいは、![]() の周期関数を用いた式(3)、
の周期関数を用いた式(3)、
![]()
もまたブロッホの定理と呼ばれることもある。このとき、ブロッホの定理を満たす ![]() をブロッホ関数と呼ぶ。
をブロッホ関数と呼ぶ。
2. ブロッホ関数を描く
絵を描いてみる。
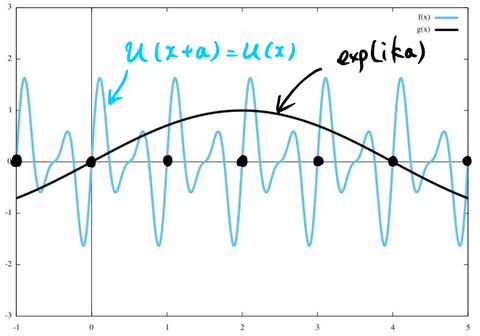
水色は周期関数 ![]() を表している。黒線は
を表している。黒線は ![]() の実部 cos(
の実部 cos(![]() ) を描いた。格子間隔は
) を描いた。格子間隔は![]() とした。周期境界条件は
とした。周期境界条件は ![]() とした。実際には、波動関数は複素数なので、複素数の形
とした。実際には、波動関数は複素数なので、複素数の形 ![]() と
と ![]() との積になる。この2つの関数の積をとって
との積になる。この2つの関数の積をとって ![]() を書き加えてみる。
を書き加えてみる。
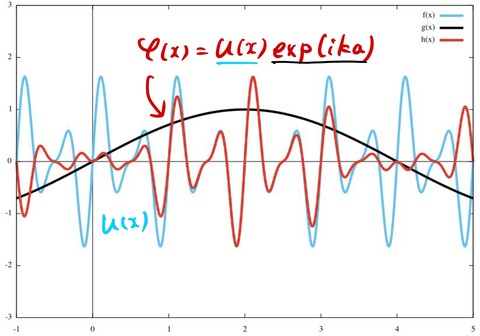
赤線が波動関数 ![]() を表したブロッホ関数である。周期関数
を表したブロッホ関数である。周期関数 ![]() が
が ![]() によって変調されている様子がわかる。
によって変調されている様子がわかる。
3. まとめ
前編はここまでで、後編では「周期境界条件」と「波数 ![]() 」の意味などを説明していきたい。
」の意味などを説明していきたい。
ブロッホ関数のプロットをしたい方:
ここでプロットに用いた関数は以下の通りで、gnuplotで簡単に書くことができます。関数系は適当なものを選択しました。
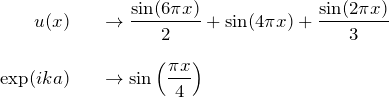
以下を参考にすればブロッホ関数が楽しめます。
set sample 500
set xrange [-1:5]
set yrange [-3:3]
set zeroaxis
tp=2*pi
f(x) = sin(tp*3*x)/2.0 + sin(2*tp*x) + sin(tp*x)/3.0
g(x) = sin(tp*x/8.0)
h(x) = (sin(tp*3*x)/2.0 + sin(2*tp*x) + sin(tp*x)/3.0)*sin(tp*x/8.0)
plot f(x) lt 3 lw 4,
g(x) lt 8 lw 4,
h(x) lt 7 lw 4