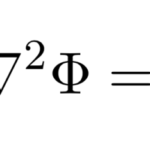端がなく周期的な系に対して、シュレディンガー方程式を解いていこう。 ここでは自由電子模型を考える。 つまり、電子が自由に動き回ることができる模型で、電子の受けるポテンシャルはゼロ(![]() )とする。
)とする。
1次元でシュレディンガー方程式を解き、その後、3次元の問題を考えていく。 式は丁寧に書いておく。
そのほかのケースは、
- 自由電子模型:無限に広い場合(3次元)
- 自由電子模型:端がない周期的な系(1次元、3次元)←
- 1次元井戸型ポテンシャル(無限井戸)
- 1次元井戸型ポテンシャル(有限井戸)
- 周期ポテンシャルのある場合(ブロッホの定理)
- クローニッヒ・ペニー模型
シュレディンガー方程式を解く
1次元から始める。
1次元の解
自由電子模型におけるシュレディンガー方程式(1次元)は
![]()
である。ポテンシャル ![]() を取っている。また、
を取っている。また、![]() は波動関数である。 この解は、
は波動関数である。 この解は、
(1) ![]()
のように平面波 ![]() の線型結合で表すことができる(
の線型結合で表すことができる(![]() の代わりに、
の代わりに、![]() で表しても良い)。
で表しても良い)。
参考:シュレディンガー方程式と自由電子模型:系が無限に広い場合
ここで、![]() に周期
に周期 ![]() があるとして、周期境界条件(1次元)
があるとして、周期境界条件(1次元)
![]()
を課す。 このとき、
![]()
より、
![]()
となる。この等式が任意の ![]() について成立するため、
について成立するため、
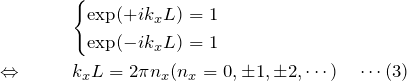
このとき、![]() を波数という。
いくつか特徴を簡単に書いておく。
を波数という。
いくつか特徴を簡単に書いておく。
-
次元:長さ
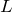 の逆次元で、逆格子空間で表す
の逆次元で、逆格子空間で表す
-
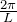 の 整数
の 整数 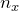 倍で表されており、離散的(とびとび)で量子化されている
倍で表されており、離散的(とびとび)で量子化されている
-
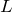 が大きいほど、
が大きいほど、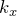 の間隔は狭い
の間隔は狭い
式(3)の波数 ![]() にある状態の波動関数を
にある状態の波動関数を
![]()
とする![]() 。いま、「
。いま、「![]() に電子が1個見出される」と規格化する
に電子が1個見出される」と規格化する![]() 。
。
![]()
より、![]() となる。 したがって、求める波動関数は
となる。 したがって、求める波動関数は
![]()
となる。また、エネルギー固有値は ![]() と量子化される。
と量子化される。
* ![]() の係数
の係数 ![]() はいつの間にか
はいつの間にか ![]() になった。その理由は、
になった。その理由は、![]() に正負の整数を許しているためである。
に正負の整数を許しているためである。
** ある領域内で規格化しておくことで、係数 ![]() を求めることができる。さもなければ全空間で積分することになり、それは無限大に発散する。
を求めることができる。さもなければ全空間で積分することになり、それは無限大に発散する。
3次元の解
3次元への拡張は簡単である。まず、周期境界条件は
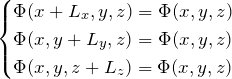
となる。したがって、波数は
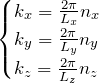
となる。 また、シュレディンガー方程式
![]()
の解は 「自由電子模型:無限に広い場合」 で求めた答えを利用すると、
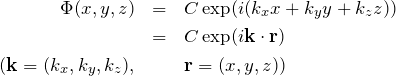
となる。
1次元の場合と同様に、![]() で規格化する。 すなわち、体積
で規格化する。 すなわち、体積 ![]() 内の空間で、波数
内の空間で、波数 ![]() の電子が1個存在するとする。
の電子が1個存在するとする。
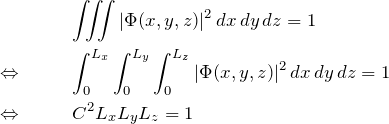
となる。よって、![]() となり、3次元の場合の波動関数を求めることができる。
となり、3次元の場合の波動関数を求めることができる。
![]()
![]() のとき、波数ベクトル
のとき、波数ベクトル ![]() は
は
![]()
となる。ここで、![]() は
は ![]() 直交座標系における単位ベクトルである。 その単位ベクトルの整数
直交座標系における単位ベクトルである。 その単位ベクトルの整数 ![]() 倍で、波数ベクトルを表すことができるため、波数ベクトルは逆格子空間における格子点で指定される。
倍で、波数ベクトルを表すことができるため、波数ベクトルは逆格子空間における格子点で指定される。
もちろんエネルギーも量子化されている。
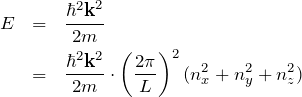
まとめ
自由電子模型では ![]() をとる。また、ここでは周期境界条件を課すことで、波動関数は平面波によって表すことができた。 実際は結晶中の電子は、原子が作るポテンシャルなどを受け
をとる。また、ここでは周期境界条件を課すことで、波動関数は平面波によって表すことができた。 実際は結晶中の電子は、原子が作るポテンシャルなどを受け ![]() となる。 たとえば、結晶に周期的なポテンシャル
となる。 たとえば、結晶に周期的なポテンシャル ![]() などがある場合はどうなるだろうか。 その話は「ブロッホの定理」と関わってくるので別に説明しよう。
などがある場合はどうなるだろうか。 その話は「ブロッホの定理」と関わってくるので別に説明しよう。
とにかく、簡単なモデルとして ![]() を仮定し、おおまかに波動関数を求めることに意味がある。 自由電子模型でシュレディンガー方程式を解くということは、より複雑な系を学ぶための土台作りになると言える。
を仮定し、おおまかに波動関数を求めることに意味がある。 自由電子模型でシュレディンガー方程式を解くということは、より複雑な系を学ぶための土台作りになると言える。