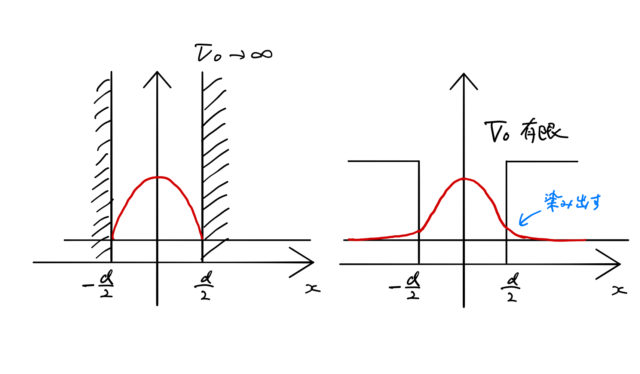
無限井戸形ポテンシャルでは電子は井戸の中に完全に閉じ込められているが、有限井戸形ポテンシャルでは井戸の外へ波動関数が染み出す。 この染み出しはトンネル効果とも関係するような量子力学的な効果であり、古典力学では見られない現象である。 この有限井戸の考え方は半導体のヘテロ接合を考える上で重要である。
- 自由電子模型:無限に広い場合(3次元)
- 自由電子模型:端がない周期的な系(1次元、3次元)
- 1次元井戸型ポテンシャル(無限井戸)
- 1次元井戸型ポテンシャル(有限井戸)←
- 周期ポテンシャルのある場合(ブロッホの定理)
- クローニッヒ・ペニー模型
問題設定
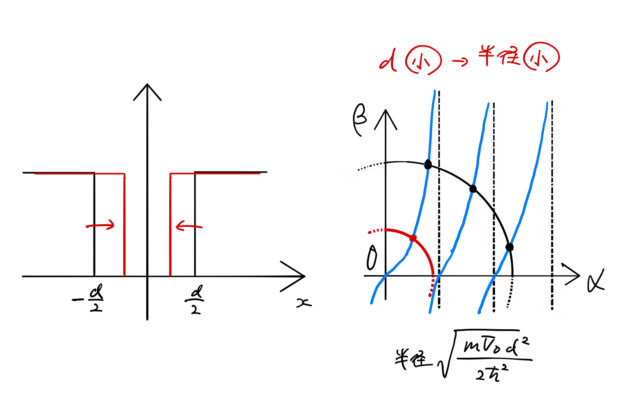
1次元の場合における有限井戸の問題設定をおこなう。有限井戸とは、図のようなポテンシャルが井戸のようになっており、井戸の深さ(高さ)が有限である井戸のことである。ここでは、エネルギーがポテンシャルより小さい場合 ![]() について見ていく。
について見ていく。
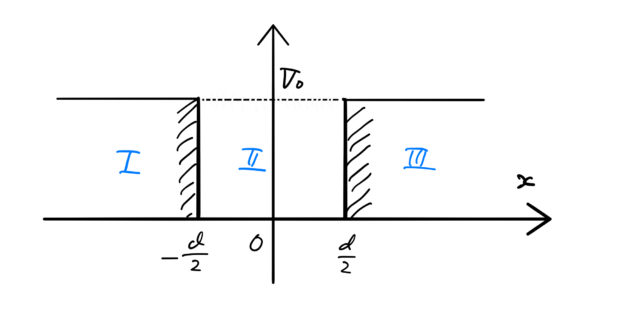
図のようにポテンシャルの深さを ![]() 、井戸の幅を
、井戸の幅を ![]() とすると、
とすると、
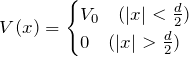
である。このとき、時間に依存しないシュレディンガー方程式
![]()
を解いて、固有状態
解答の流れ以下の通りである。
- 3つの領域で波動関数を求める
- 境界条件により波動関数を決定する
- 固有エネルギーを求める
領域ごとに波動関数を決める
![]() に対応する井戸の内側の領域が最も簡単なので、領域
に対応する井戸の内側の領域が最も簡単なので、領域![]() から解いていく。
領域 I と領域
から解いていく。
領域 I と領域 ![]() はほとんど同じである。
はほとんど同じである。
領域II
この領域では ![]() であるためシュレディンガー方程式は
であるためシュレディンガー方程式は
![]()
となる。これは自由電子のシュレディンガー方程式であり、その固有状態は平面波
平面波の波数 ![]() を
を
![]()
と定義すると、固有状態である波動関数は
![]()
である。
領域I
この領域では ![]() である。シュレディンガー方程式は
である。シュレディンガー方程式は
![Rendered by QuickLaTeX.com \begin{eqnarray*} && \left[-\frac{\hbar^2}{2m}\frac{d^2}{dx}+V_0\right]\psi_{\rm I}(x)=E\psi_{\rm I}(x)\\ \Leftrightarrow\quad&& \textcolor{red}{+}\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi_{\rm I}(x)=(V_0-E)\psi_{\rm I}(x) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8f2654ae2e04a01c12fca66992d1f25a_l3.png)
である。この微分方程式の解は、平面波
![]()
である(![]() は定数)。
は定数)。![]() は平面波
は平面波 ![]() に対応する実数で、
に対応する実数で、
![]()
とした。波動関数が無限遠 ![]() で収束するためには、指数関数
で収束するためには、指数関数 ![]() の係数について
の係数について ![]() でなければならない。
でなければならない。 ![]() を
を ![]() と書き換えて、領域Iの波動関数は
と書き換えて、領域Iの波動関数は
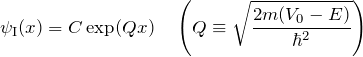
となる。定数 ![]() は境界条件によって決定される。
は境界条件によって決定される。
領域III
この領域は領域Iと同様のシュレディンガー方程式であり、波動関数は
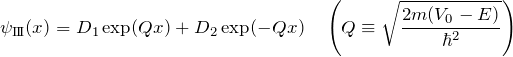
である(
![]()
となる。定数
境界条件
それぞれの波動関数 ![]() をまとめておくと、
をまとめておくと、
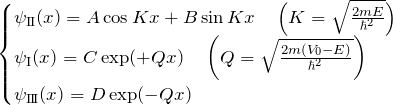
となる。
領域が3つに分けられているため、2つの境界があり、それぞれの境界で波動関数が連続でかつ滑らかでないといけない。 したがって、境界条件は 領域Iと領域![]() の境界で、連続かつ滑らかである(微分係数が等しい)ことから
の境界で、連続かつ滑らかである(微分係数が等しい)ことから
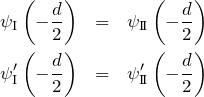
となる。領域
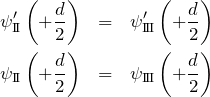
となる。以上4つの条件から定数
具体的に代入すると
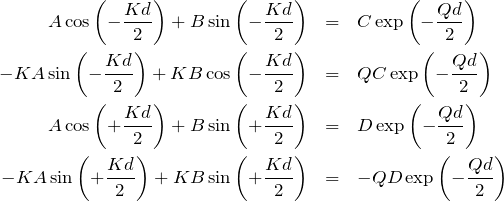
となる。 4式から
これを具体的に解いていく。
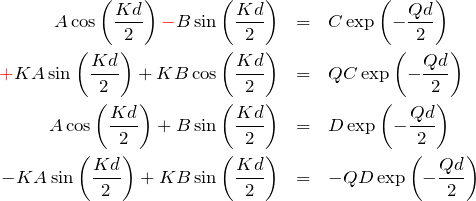
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[ Q\cos\left(\frac{Kd}{2}\right)-K\sin \left(\frac{Kd}{2}\right)\right]A\textcolor{red}{-} \left[ Q\sin \left(\frac{Kd}{2}\right)+K\cos\left(\frac{Kd}{2}\right)\right]B=0\\ \left[ Q\cos\left(\frac{Kd}{2}\right)-K\sin \left(\frac{Kd}{2}\right)\right]A\textcolor{red}{+} \left[ Q\sin \left(\frac{Kd}{2}\right)+K\cos\left(\frac{Kd}{2}\right)\right]B=0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9dd0bdf7e3f84fecada08a5f18ec5dc5_l3.png)
となる。(上式)
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\left[ Q\cos\left(\frac{Kd}{2}\right)-K\sin \left(\frac{Kd}{2}\right)\right]A=0\quad\cdots \quad(1)\\ &&\left[ Q\sin \left(\frac{Kd}{2}\right)+K\cos\left(\frac{Kd}{2}\right)\right]B=0\quad\cdots \quad(2) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f47939dbb67bc22606a6f23e7095b782_l3.png)
実際、(i)
![]()
となるが、(2)から
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&B\left[ Q\sin \frac{Kd}{2}+\frac{K^2}{Q}\sin \left(\frac{Kd}{2}\right) \right]=0\\ \Leftrightarrow \quad && B\frac{Q^2+K^2}{Q^2}\sin \left(\frac{Kd}{2}\right)=0\quad(\because {\rm Eq.} (3)) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8de51da6289aeedb3a70f71c3fb18a92_l3.png)
となる。
![]()
となり、このとき
また、(ii)
![]()
より、式(1)から
![]()
となる。
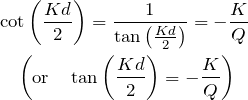
このとき、
(i) ![]() に対して、
に対して、
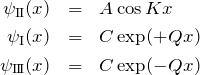
である。このとき、
![]()
を満たす。
また、(ii) ![]() に対して、
に対して、
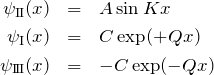
このとき、
![]()
を満たす。
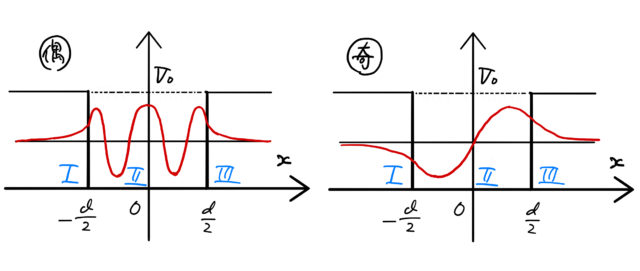
図のように(i)の波動関数は偶関数であり、(ii)の波動関数は奇関数になっている。
エネルギーを求める
![]() ,
, ![]() より、
より、![]() を求めることで
を求めることで ![]() が決定できる。
が決定できる。 ![]() の関係は上で求めた
の関係は上で求めた ![]() の式に加えて、
の式に加えて、
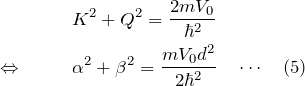
の関係がある。簡単のため、
![]()
と置いた。式(5)は
このとき、(i)の波動関数に対する連立方程式
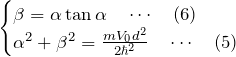
または、(ii)の波動関数に対する連立方程式
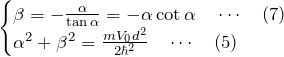
を満たす
![]()
より
図の![]() は(i)偶関数の場合(
は(i)偶関数の場合(![]() の条件式)に対応し、
の条件式)に対応し、![]() は(ii)奇関数の場合(
は(ii)奇関数の場合(![]() の条件式)に対応する。いま5つの交点があり、それぞれの交点に対応してエネルギー固有値
の条件式)に対応する。いま5つの交点があり、それぞれの交点に対応してエネルギー固有値 ![]() と波動関数が定められる。
と波動関数が定められる。
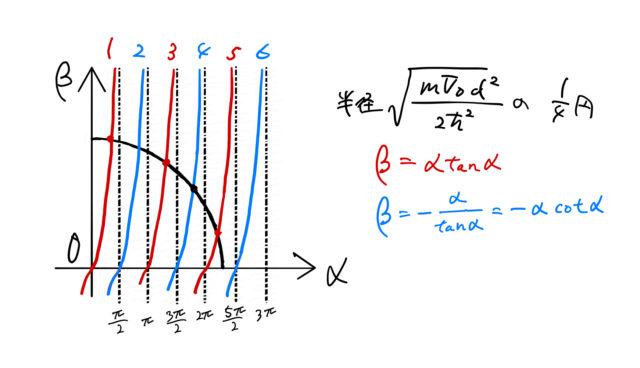
dやV0を変えてみる
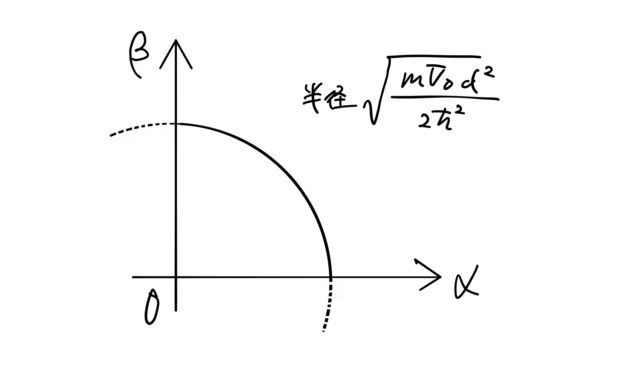
![]() より式(5)は1/4円(第一象限)を表しており、その半径は井戸の幅
より式(5)は1/4円(第一象限)を表しており、その半径は井戸の幅 ![]() と深さ
と深さ ![]() に依存する。
に依存する。 ![]() を小さくしていくと、図のように円の半径は小さくなる。
を小さくしていくと、図のように円の半径は小さくなる。![]() がある程度大きな場合は複数個の交点を持つ。図のような3つの交点のエネルギーに対応する状態は3つある(波動関数は(i)2つの偶関数と(ii)1つの奇関数)。
がある程度大きな場合は複数個の交点を持つ。図のような3つの交点のエネルギーに対応する状態は3つある(波動関数は(i)2つの偶関数と(ii)1つの奇関数)。
半径が小さくなる(井戸を狭くする)につれて、![]() との交点の数は減っていく。しかし、
との交点の数は減っていく。しかし、![]() は原点を通る関数であるため、どれだけ小さな半径をもつ円に対しても
は原点を通る関数であるため、どれだけ小さな半径をもつ円に対しても ![]() に交点は存在する。したがって、少なくとも1つの固有状態が存在することがわかる。
に交点は存在する。したがって、少なくとも1つの固有状態が存在することがわかる。
この ![]() が小さく交点が1つしかない場合における波動関数は偶関数である。 なぜなら、交点ができるのは
が小さく交点が1つしかない場合における波動関数は偶関数である。 なぜなら、交点ができるのは ![]() に対応する式であり、この式は(i)
に対応する式であり、この式は(i)![]() の場合に対応するためである。
の場合に対応するためである。
また、有限井戸型ポテンシャルの場合では波動関数が井戸の外でも 0 になっていないことを確認しておく。
![]()
その波動関数は原点から離れるにつれて指数関数的に減衰するが、粒子の存在確率を表す波動関数の絶対値の2乗が0でないことが確認でき、波動関数が染み出していることがわかる。 これは古典論には見られない現象で、壁を越えるだけのエネルギーがなくても壁を超えたところに有限の存在確率をもっていることを意味する、量子力学的な現象である。
次に ![]() としてみると、これは井戸の深さを無限にする無限井戸型ポテンシャルに対応する。このとき
としてみると、これは井戸の深さを無限にする無限井戸型ポテンシャルに対応する。このとき ![]() より、
より、![]() つまり
つまり ![]() となり、無限井戸型ポテンシャルの場合の波動関数に対応する。無限井戸の場合は、有限井戸のときのように波動関数は井戸の外へは染み出さない。
となり、無限井戸型ポテンシャルの場合の波動関数に対応する。無限井戸の場合は、有限井戸のときのように波動関数は井戸の外へは染み出さない。
\end{document}