【振動】周期的な力F(t)の強制振動(摩擦無し)の運動方程式と一般解
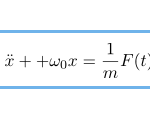
振動は物理において重要な運動である。ここでは摩擦の項がない(減衰のない)強制振動の運動方程式(以下の式)をラグランジアンから導出して、一般解を考える。物理現象としては「共鳴」や「 うなり 」に関係する。 ポイント &n …
もっと読む 【振動】周期的な力F(t)の強制振動(摩擦無し)の運動方程式と一般解バター猫のパラドックス
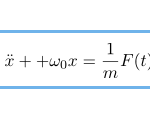
振動は物理において重要な運動である。ここでは摩擦の項がない(減衰のない)強制振動の運動方程式(以下の式)をラグランジアンから導出して、一般解を考える。物理現象としては「共鳴」や「 うなり 」に関係する。 ポイント &n …
もっと読む 【振動】周期的な力F(t)の強制振動(摩擦無し)の運動方程式と一般解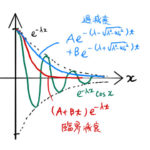
減衰振動は自由振動(単振動)の運動に、摩擦による抵抗の項を加えた運動になっている。減衰振動においては、振動の振幅がどんどん小さくなっていき最後には止まってしまう。 【参考】例題で学ぶ:ラプラス逆変換(振動運動の微分方程 …
もっと読む 【振動】減衰振動/臨界振動/過減衰の運動方程式と一般解、そのイメージ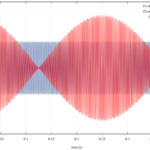
強制振動とは、ブランコに乗っている人を後ろから押してやるみたいに、振動数 で自由振動している系を外場 によって強制的に振動させる運動のことである。もともとの に近い振動数で外場 を与えたときには「うなり」が発生する。以 …
もっと読む 【振動】「うなり」と強制振動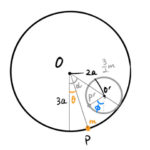
微小振動の例として円筒振り子がある。この円筒振り子の中にさらに円柱を入れて2つの微小振動を見る。以下の例題で考える。 左が厚みのない円筒の振り子。右が円筒振り子内の円柱(灰色)。 半径 の円筒振り子の軸まわりの慣性モ …
もっと読む 【振動】円筒振り子の中の円柱(微小振動)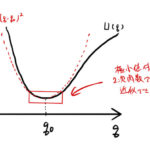
1次元の自由振動は単振動と呼ばれ、高校物理でも一応は扱う。ここで学ぶ自由振動は下に挙げた減衰振動、強制振動などの基礎になる。上の4つの振動は変位 が微小のときの話である。 自由振動(単振動): 減衰振動: 強制振動( …
もっと読む 【振動】1次元の自由振動(単振動)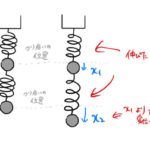
連成振動とは、バネで繋がった2個以上の質点が互いに相互作用しながら運動する振動のことである。質点が1個だけのときの振動より複雑になる。 質点2個の場合の連成振動(垂直型)の運動方程式を立てて解いていく。バネの復元力の …
もっと読む 【振動】垂直にバネで繋がった2質点の連成振動:運動方程式の立て方・解き方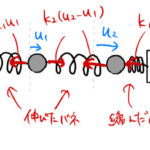
連成振動とは、バネで繋がった2個以上の質点が互いに相互作用しながら運動する振動のことである。質点が1個だけのときの振動より複雑になる。 質点2個の場合の連成振動の運動方程式を立てて解いていく。バネの復元力の向きがどっ …
もっと読む 【振動】水平に置かれた2質点の連成振動:運動方程式の立て方・解き方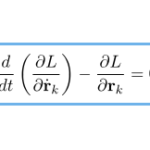
ここでは、「最小作用の原理 」によってラグランジュ方程式を導くことはしない。単に、「ニュートンの運動方程式 → ラグランジュ方程式」をおこなう。 よく知られているように1個の質点に対して運動方程式は、 …
もっと読む 【解析力学】運動方程式からラグランジュ方程式を導出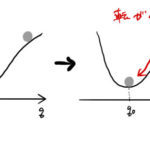
バネの弾性エネルギーは で与えられている。これは変位が小さいという仮定で成り立つ話である。バネの復元力が変位に比例するとしてフックの法則もまた、変位が小さいところで成り立つ。 どのようにして出てきたか、ポテンシャルエ …
もっと読む 【解析力学】何故バネの弾性エネルギーはxの2乗に比例するか(調和項・非調和項)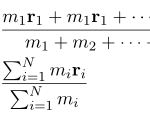
1体問題、2体問題、 体問題の運動方程式について簡単にまとめておく。 質点と運動方程式 体問題では、個の質点の運動方程式を考える。物理で考える場合は、 の1体問題、 の2体問題、 が3以上の多体問題 しかない。われわれ人 …
もっと読む 【古典力学】1体問題、2体問題、N体問題の運動方程式