バネの弾性エネルギーは 
で与えられている。これは変位が小さいという仮定で成り立つ話である。バネの復元力が変位に比例するとしてフックの法則もまた、変位が小さいところで成り立つ。
どのようにして出てきたか、ポテンシャルエネルギーに注目して説明する。
1. ボールは低いところに
図の左のように、谷のある場所に灰色のボールを置く。そうすると右のようにボールは極小値の位置に転がる。
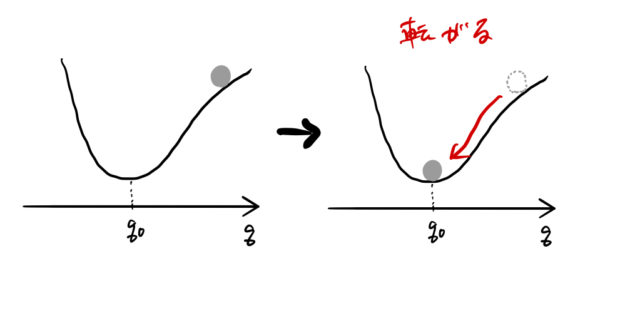
この図において横軸 
は位置を表しており、極小値は 
である。谷に摩擦がない場合は、ボールは左側までいって初めの一と同じ高さまでのぼるだろう。
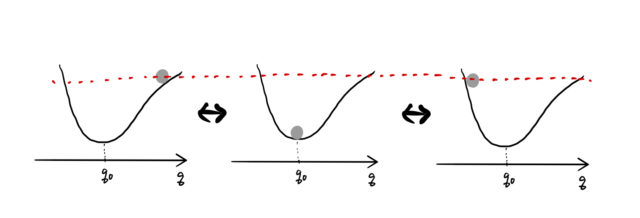
これもまた振動的な運動である。しかし、谷の形が左右非対称になっているため、
の簡単な振動ではないように見える。これは非調和振動と呼ぶ。非調和振動が現れているのは、高い位置からボールを離してしまったからである。
もっと低い位置からボールを離せば、調和振動（よくある単振動）とみなすことができる。すなわち、極小値をとる 
からあまり離れていないところの話になる。
2. ポテンシャルエネルギー
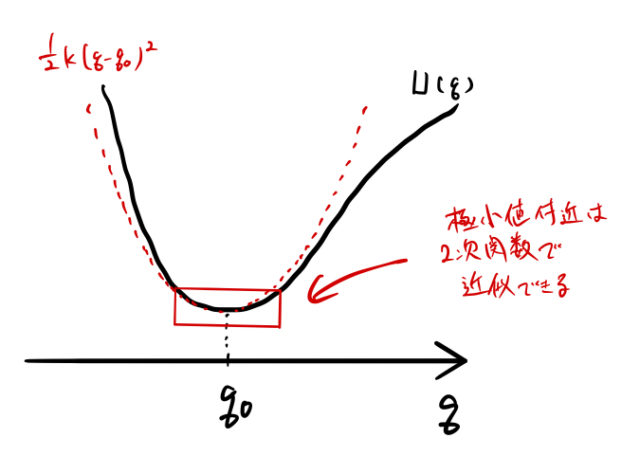
上に示した「谷」はポテンシャルエネルギー 
と考えることができる。そして 周りで谷の形が放物線（２次関数）になることを示す。
2.1 釣り合いの位置まわりで展開
ポテンシャルの極小値は である（１階微分が0）：
ポテンシャルを 周りでテイラー展開する
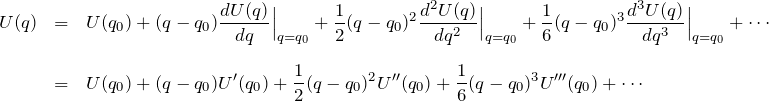
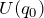：これはポテンシャルの原点で 0 にとる。基準は勝手に決めて良い。これは、無限遠を０にとった静電ポテンシャルと似ている。
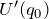：ポテンシャルの極小値だから 0 。
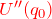：一般には 0 ではない。
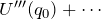：より高次の項
結局 残るのは
である。
を釣り合いの位置からの変位とすると 
である。関数が
※
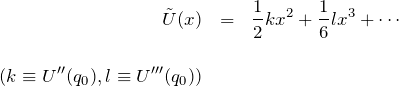
とした理由：ポテンシャルの形は同じだが、 分だけずれている。したがって、 と関数が異なるためここではちゃんと書いた。
2.2 調和項・非調和項
変位 が小さい場合：
- よくみる弾性エネルギーの形 (
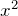に比例) - 単振動（調和振動、自由振動）のポテンシャル
- フックの法則：
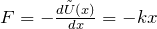
変位 が大きい場合：
- 高次の項が効いてくる (
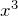に比例する非調和項など) - 非調和振動
3. まとめ
非調和項が必要となるのは、変位が大きい場合である。変位が小さい場合は、ポテンシャルは に比例する形で近似できる。これが、弾性エネルギーが になる理由である。