ここでは、「最小作用の原理 」によってラグランジュ方程式を導くことはしない。単に、「ニュートンの運動方程式 → ラグランジュ方程式」をおこなう。
よく知られているように1個の質点に対して運動方程式は、
![]()
である。座標系は、![]() のようにデカルト座標系でとっている。
のようにデカルト座標系でとっている。
質点が![]() 個ある場合は、インデックス
個ある場合は、インデックス ![]() をつければよい。したがって運動方程式は
をつければよい。したがって運動方程式は ![]() 個ある。
個ある。
![]()
以下では運動エネルギーとポテンシャルを ![]() で表す。
で表す。
運動エネルギー ![]() :
:
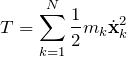
ポテンシャル ![]() は
は ![]() を保存力として以下のように与えられるとする。
を保存力として以下のように与えられるとする。
![]()
この保存力とポテンシャルの関係がわかりにくい場合は、重力 ![]() と位置エネルギー
と位置エネルギー ![]() の関係を思い出してほしい。
の関係を思い出してほしい。
運動量 ![]() の時間微分を 運動エネルギー
の時間微分を 運動エネルギー ![]() で表す。
で表す。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{d}{dt}{\bf p}_k &=&\frac{d}{dt}\left[\frac{\partial}{\partial \dot{\bf x}_k} \frac{1}{2}m_k \dot{bf x}_k^2 \right]\\\\ &=& \frac{d}{dt}\left[\frac{\partial}{\partial \dot{\bf x}_k} \sum_{j=1}^{N} \frac{1}{2}m_j \dot{\bf x}_j^2 \right] \\ &&(\because \frac{\partial}{\partial \dot{\bf x}_k} \dot{\bf x}_j^2=0 \quad {\rm if}\quad j\neq k)\\\\ &=& \frac{d}{dt}\frac{\partial T}{\partial \dot{\bf x}_k} \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-d3b54d7264391a6d9e9ccc0c96483573_l3.png)
以上より、ニュートンの運動方程式に戻って、
![]()
この左辺は運動エネルギー ![]() で表すことができた。
で表すことができた。
![]()
便利な表記として、
![]()
を導入すると、
![]()
これよりラグランジアンを定義する。ラグランジアン ![]() を
を
![]()
のように定義する。運動エネルギーは速度のみ、ポテンシャルは位置のみ関数となっている。したがって、ラグラジアンにより式(1)は、
![]()
で表されたラグランジュ方程式(オイラー・ラグランジュ方程式)が導かれる。![]()
ここで、![]() であったため、上のラグランジュ方程式は
であったため、上のラグランジュ方程式は ![]() 個ある。また、
個ある。また、![]() が3次元の座標の場合は
が3次元の座標の場合は ![]() 個の方程式ができる。
個の方程式ができる。
最後に簡単にラグランジュ方程式とニュートンの運動方程式の違いを述べる。ニュートンの運動方程式は デカルト座標(![]() ) のみで簡単な形になっている。ニュートンの運動方程式を極座標に直すのは少々の計算が必要である。
) のみで簡単な形になっている。ニュートンの運動方程式を極座標に直すのは少々の計算が必要である。
一方で、最後に得たラグランジュ方程式は座標系の取り方によらず同じ形になっている。問題が解きやすい座標系を考えて、系のラグランジアン ![]() を与えることで、ニュートンの運動方程式と等価な方程式を考えていることになる。
を与えることで、ニュートンの運動方程式と等価な方程式を考えていることになる。