【複素積分】応用(三角関数(cos,sin)型の実積分の変換)
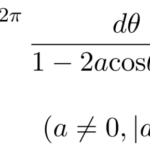
複素積分の応用問題を解く。 ここで学ぶことは、 留数定理の応用 実積分を複素積分で解く である。 有名な問題としてを積分しよう。 例題 (1)
もっと読む 【複素積分】応用(三角関数(cos,sin)型の実積分の変換)バター猫のパラドックス
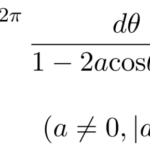
複素積分の応用問題を解く。 ここで学ぶことは、 留数定理の応用 実積分を複素積分で解く である。 有名な問題としてを積分しよう。 例題 (1)
もっと読む 【複素積分】応用(三角関数(cos,sin)型の実積分の変換)例題として、以下の3問を見ていく。ローラン展開→複素積分の流れで計算した。したがって、複素積分の計算に「留数定理」は使わなかった。参考:「例題で学ぶ:ローラン展開/極/留数定理」 (読了目安:30分) 例題 Cを|z| …
もっと読む 【複素積分】「sin(z)/z」「e^z/z」「1/z^3」のローラン展開/ 複素積分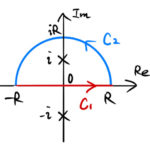
複素積分の応用例として、以下の実積分を複素積分で解く。ちなみにこの実積分は講義積分で、 とすれば容易に解ける。 複素積分の例題 以下の実積分を複素積分を用いて解け(積分経路は少し下に与えた)。   …
もっと読む 【複素積分】f(x)=1/(1+x^2)の実積分(-∞,∞)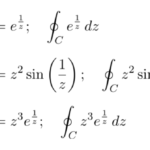
ローラン展開例題シリーズその3。ここまで、ローラン展開の基本と例題 、三角関数を含んだ関数のローラン展開の例題 を扱ってきた。ここでは が真性特異点である複素関数について、ローラン展開して複素積分を求める。孤立特異点に …
もっと読む 【例題で学ぶ③】ローラン展開/複素積分の例題(「sin(1/z)」「e^(1/z)」など真性特異点を持つ関数型)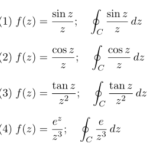
ローラン展開例題シリーズその2。その1で 「ローラン展開の基本と例題」 を扱った。ここでは例題を使って、三角関数が入った複素関数をローラン展開する。 目標:ローラン展開ができるようになる。それを利用して複素積分ができるよ …
もっと読む 【例題で学ぶ②】ローラン展開/複素積分の例題「sinz/z」「cosz/z」「tanz/z^2」など三角関数型)
ローラン展開例題シリーズその1。ローラン展開の基本を簡単な例題で学ぶ。ここで扱うのは初歩的な話と初歩的な例題である。厳密な説明、発展的な例題は教科書に載っているだろう。 ローラン展開の例題 次の関数 を与えられた点の周 …
もっと読む 【例題で学ぶ①】ローラン展開/わかりやすい基本と例題/テイラー展開との違い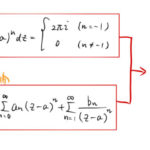
ここでは「留数定理」という名前から来る仰々しさと「ローラン展開」の妖艶さについて、例題からわかりやすく解説する。まずは、もっとも簡単な1位の極の例題を解いていこう。 目標:ローラン展開 → 留数定理の流れを理解する。 …
もっと読む 【例題で学ぶ⓪】ローラン展開/極/留数定理