ローラン展開例題シリーズその1。ローラン展開の基本を簡単な例題で学ぶ。ここで扱うのは初歩的な話と初歩的な例題である。厳密な説明、発展的な例題は教科書に載っているだろう。
次の関数 ![]() を与えられた点の周りでローラン展開せよ。
を与えられた点の周りでローラン展開せよ。
(1) ![]()
(2) ![]()
(3) ![]()
1. ローラン級数展開の定義
複素平面内の領域 ![]() で関数
で関数 ![]() が、点
が、点 ![]() を除いて正則であるときに次のようにローラン展開できる。
を除いて正則であるときに次のようにローラン展開できる。
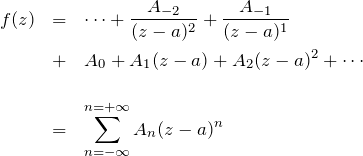
ここで展開係数 ![]() は、
は、
![]()
である。![]() は
は ![]() 含む閉曲線(領域
含む閉曲線(領域 ![]() 内)。
内)。
実際、このまじめな式はあまり使わない(特に定期試験や院試などで)。
2. ローラン級数展開の概要
いつローラン展開?
ローラン展開は複素関数の特異点周りで展開する。特に複素積分を行う場合に有用である。一般に ![]() の形が複雑だったりすると、
の形が複雑だったりすると、
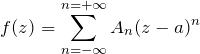
にしておくと、![]() がわかりやすい。
がわかりやすい。
なぜローラン展開?
テイラー展開と同様に、簡単な形に展開しておくと微分・積分が実行しやすくなる。とくに、複素積分は応用の上でも重要である。ここでは、ローラン展開による恩恵を少し書いておきたい。
下のような計算があったことを思い出そう。
![]()
なんとなく
のように展開すると ![]() の中に
の中に ![]() があって、積分の見通しがよくなる気がしないだろうか。例えば、
があって、積分の見通しがよくなる気がしないだろうか。例えば、
![]()
のようになる。さらに、ここで ![]() が出てきたのは留数定理のように見える。
が出てきたのは留数定理のように見える。
※ 実際に![]() は孤立特異点
は孤立特異点 ![]() の留数である。ローラン展開と留数定理の話については留数定理のところで扱いたい。(参考:例題で学ぶ:ローラン展開/極/留数定理(読了目安:15~30分))
の留数である。ローラン展開と留数定理の話については留数定理のところで扱いたい。(参考:例題で学ぶ:ローラン展開/極/留数定理(読了目安:15~30分))
ローラン展開とテイラー展開の違い
ざっくり違いを説明する。下は2変数の実関数 ![]() を表す。
を表す。
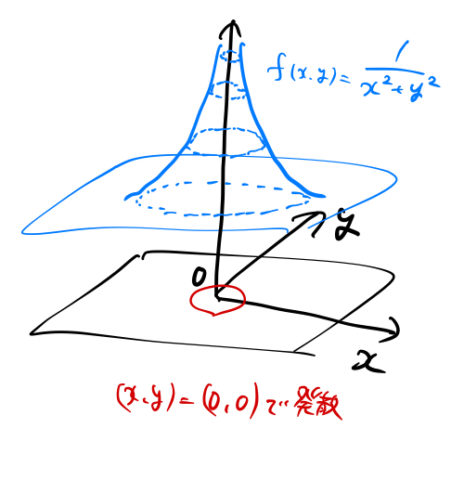
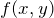
図は実関数であるが、イメージとして似ている。テイラー展開は特異点でない![]() 周りで展開する。例えば、
周りで展開する。例えば、![]() 周りとかで。
周りとかで。
- ローラン展開:ある特異点
 周りで展開
周りで展開 - テイラー展開:ある正則な点 周りで展開
例えば、複素関数のテイラー展開は
![]()
もし右辺に、![]() などの分母に
などの分母に ![]() の形を含む項があれば、ローラン展開のように
の形を含む項があれば、ローラン展開のように ![]() で特異点になっているはずである。
で特異点になっているはずである。
![]() とすれば左辺の
とすれば左辺の ![]() は正則であるため、そのような項はでないはず。
は正則であるため、そのような項はでないはず。
一方ローラン展開は ![]() が孤立特異点である。
が孤立特異点である。
とすると、![]() について左辺も右辺も特異的である。
について左辺も右辺も特異的である。
2. 例題の解答
まじめな式はあまり使わない。ここでは級数を利用したローラン展開を示す。
(1) の解答
![]() の
の ![]() 周りのローラン展開:
周りのローラン展開:
すでに ![]() は
は ![]() 周りでローラン展開されている。つまり、
周りでローラン展開されている。つまり、![]() で残りの展開係数
で残りの展開係数 ![]() 。
。
![]()
(2) の解答
![]() の
の ![]() 周りのローラン展開:
周りのローラン展開:
ローラン展開する。コツは ![]() は素材のままで。
は素材のままで。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{1}{z(z+1)}&=&\textcolor{red}{\frac{1}{z}\cdot\frac{1}{z+1}} \\ \\ &=& \frac{1}{z} \left[1-z+z^2-z^3+\cdots \right] \\ \\ &=& \frac{1}{z}-1+z-z^2+\cdots \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-78d42a9be0485a3c89db7f341a4d94cd_l3.png)
ここで、![]() における級数展開:
における級数展開:
![]()
を用いた。
最後の答えは、![]() などで答えても良い。
などで答えても良い。
(3) の解答
![]() の
の ![]() 周りのローラン展開:
周りのローラン展開:
![]() が素材である。基本的に
が素材である。基本的に ![]() の形を作るように変形する。
の形を作るように変形する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{z}{(z+1)(z+2)} &=& \frac{1}{z+1}\cdot\frac{z}{z+2}\\\\ &=& \frac{1}{z+1}\left[\frac{\textcolor{red}{(z+1)}-1}{\textcolor{red}{(z+1)}+1}\right]\\\\ &=& \frac{1}{z+1}\left[(z+1)-1\right]\left[ 1-(1+z)+(1+z)^2-(1+z)^3+\cdots\right]\\\\ &=& \frac{1}{z+1}\left[-1+2(z+1)-2(z+1)^2+2(z+1)^3-\cdots\right] \\ \\ &=& -\frac{1}{z+1}+2-2(z+1)+2(z+1)^2-\cdots \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-3ad06066d3bb9b3afed33d4dafcf1edf_l3.png)
初めのうちは、![]() 周りのローラン展開になるように
周りのローラン展開になるように ![]() などと置いて変形したほうがわかりやすいかもしれない。
などと置いて変形したほうがわかりやすいかもしれない。
3. まとめ
例題を通して、簡単なローラン展開を説明した。基本的にテストや院試で出題されるローラン展開の問題は級数展開を用いるのが良い。
ローラン展開の活躍の場は留数定理である。基本に慣れたら次は三角関数である。下の「ローラン展開例題シリーズその2」へ続く。