ローラン展開例題シリーズその２。その１で 「ローラン展開の基本と例題」 を扱った。ここでは例題を使って、三角関数が入った複素関数をローラン展開する。
目標：ローラン展開ができるようになる。それを利用して複素積分ができるようになる。
次の複素関数 
を 
周りでローラン展開せよ。その後、それらの複素積分を求めよ。
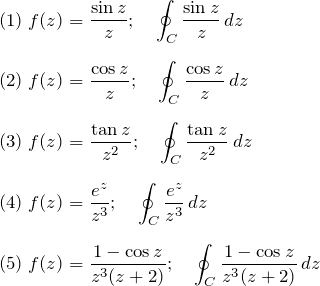
（積分経路
（反時計回り）で、以下同様。）目次
1. マクローリン展開まとめ
解答で使う三角関数と指数関数の展開をまとめておく。
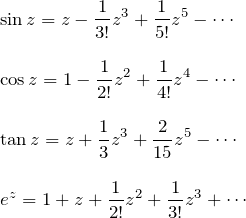
2. 解答
複素積分の計算の方針：
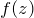- をローラン展開する
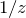の係数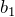 
（留数）を求める- 複素積分の値は 「
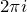×（留数）」（留数定理）
なぜこれで求められるかは、「例題で学ぶ：ローラン展開／極／留数定理」 に書いた。（読了目安：15~30分）
(1) f(z) = sin(z)/z
ローラン展開の方針： はそのまま使う。
- ローラン展開：
![\begin{eqnarray*} \frac{\sin z}{z}&=&\frac{1}{z}\cdot\sin z\\\\ &=&\frac{1}{z}\left[z -\frac{1}{3!}z^3 + \frac{1}{5!}z^5 -\cdots\right]\\\\ &=&1 -\frac{1}{3!}z^2 + \frac{1}{5!}z^4 -\cdots\quad \blacksquare\\\\\\ \Biggl(&=&\textcolor{red}{\frac{0}{z}}+1-\frac{1}{3!}z^2 + \frac{1}{5!}z^4 -\cdots\Biggr) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e26699fe384e1a93e4a9ea5b1e0c0875_l3.png "Rendered by QuickLaTeX.com")
2. の係数 （留数）： 
がないため極なし。
3. 複素積分の値は 「 ×（留数）」：
(2) f(z) = cos(z)/z
ローラン展開の方針： はそのまま使う。
- ローラン展開：
![\begin{eqnarray*} \frac{\cos z}{z}&=&\frac{1}{z}\cdot\cos z\\\\ &=&\frac{1}{z}\left[1 -\frac{1}{2!}z^2 + \frac{1}{4!}z^4 -\cdots\right]\\\\ &=& \textcolor{red}{\frac{1}{z}} -\frac{1}{2!}z + \frac{1}{4!}z^3 -\cdots\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2cce2cc1f606bb420341a9e9cbcbd8f7_l3.png "Rendered by QuickLaTeX.com")
2. の係数 （留数）： 
は１位の極。
3. 複素積分の値は 「 ×（留数）」：
(3) f(z) = tan(z) / z^2
- ローラン展開：
![\begin{eqnarray*} \frac{\tan z}{z^2}&=&\frac{1}{z^2}\cdot\tan z\\\\ &=&\frac{1}{z^2}\left[z +\frac{1}{3}z^3 + \frac{2}{15}z^5 -\cdots\right]\\\\ &=& \textcolor{red}{\frac{1}{z}} +\frac{1}{3}z + \frac{2}{15}z^3 -\cdots\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-326832118530476ffde38c87114aba3f_l3.png "Rendered by QuickLaTeX.com")
2. の係数 （留数）：
は１位の極。
3. 複素積分の値は 「 ×（留数）」：
※ 問題に関係ないが、 
の特異点は無数にある。つまり、
となるのは
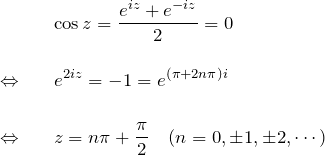
で孤立特異点が無数にある。
(4) f(z) = e^z / z^3
ローラン展開の方針：
をそのまま使う。
- ローラン展開：
![\begin{eqnarray*} \frac{e^z}{z^3}&=&\frac{1}{z^3}\cdot e^z\\\\ &=&\frac{1}{z^3}\left[1+z+\frac{1}{2!}z^2+\frac{1}{3!}z^3+\frac{1}{4!}z^4\cdots\right]\\\\ &=& \textcolor{blue}{\frac{1}{z^3}}+ \frac{1}{z^2} +\textcolor{red}{\frac{1}{2}\,\frac{1}{z}} + \frac{1}{6}+\frac{1}{24}z -\cdots\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-858eb869539cde34769922f9a989878d_l3.png "Rendered by QuickLaTeX.com")
2. の係数 （留数）： 
の項が残っているため、 は3位の極。
3. 複素積分の値は 「 ×（留数）」：
【別解】 「留数定理」 を使う。
の （３位の極）について：
![\begin{eqnarray*} \oint_C \frac{e^z}{z^3} \, dz &=&\frac{2\pi i}{(3-1)!}\lim_{z\to 0}\frac{d^2}{dz^2} \left[z^3 f(z)\right]\\\\ &=&\pi i \lim_{z\to 0}\frac{d^2}{dz^2}\left[e^z\right]\\\\ &=&\pi i \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0f8e96dec3e12af0bf1f09c9d955ccdc_l3.png "Rendered by QuickLaTeX.com")
(5) f(z) = ( 1-cos(z) ) / z^3 (z+2)
発展的な問題として出題した。
ローラン展開の方針： はそのまま使う。
- ローラン展開：
![\begin{eqnarray*} \frac{1-\cos z}{z^3(z+2)} &=&\frac{1}{2z^3}\cdot\frac{\textcolor{blue}{1-\cos z}}{\textcolor{green}{\frac{z}{2}+1}}\\\\ &=& \frac{1}{2z^3}\left[\textcolor{blue}{1-\left(1-\frac{1}{2!}z^2-\frac{1}{4!}z^4+\cdots}\right) \right]\\ &&\quad\quad\times \left[\textcolor{green}{1-\frac{z}{2}+\frac{z^2}{2^2}-\frac{z^3}{2^3}+\cdots}\right]\\\\ &=& \frac{1}{2z^3}\left[\frac{z^2}{2}-\frac{z^4}{24}+\cdots\right] \left[1-\frac{z}{2}+\frac{z^2}{4}-\frac{z^3}{8}+\cdots\right]\\\\ &=& \frac{1}{2z^3}\left\{ \frac{z^2}{2}-\frac{z^3}{4}+\left(\frac{z^4}{8}-\frac{z^4}{24}\right)\cdots\right\}\\\\ &=& \textcolor{red}{\frac{1}{4}\cdot \frac{1}{z}} -\frac{1}{8}+\frac{1}{12}z+\cdots \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-87d417c302837f97a5cb08ab5637cc5c_l3.png "Rendered by QuickLaTeX.com")
2. の係数 （留数）： 
は１位の極。
3. 複素積分の値は 「 ×（留数）」：
留数定理を使っても解ける。
3. まとめ
ローラン展開の例題として三角関数のものを扱った。ローラン展開を利用して留数を求めることで、複素積分を計算することができただろう。留数が複数ある場合はそれぞれ 倍して足し合わせる必要がある。
ローラン展開 → 複素積分 の流れは真性特異点を領域内に含んだ積分経路のときに真価を発揮する。それは以下の「ローラン展開例題シリーズその３」で扱う。