ここでは「留数定理」という名前から来る仰々しさと「ローラン展開」の妖艶さ![]() について、例題からわかりやすく解説する。まずは、もっとも簡単な1位の極の例題を解いていこう。
について、例題からわかりやすく解説する。まずは、もっとも簡単な1位の極の例題を解いていこう。
目標:ローラン展開 → 留数定理の流れを理解する。
複素積分を計算せよ。
![]()
目次
1. 前提知識
※このページでは、複素積分 ![]() は内部に特異点
は内部に特異点 ![]() を含んだ反時計回りの円を考える。
を含んだ反時計回りの円を考える。
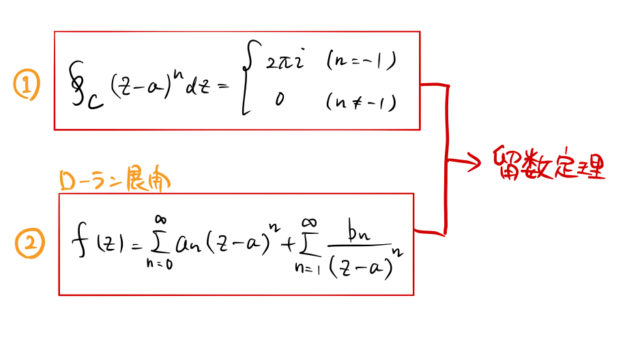
このページで留数定理を学ぶために2つのことを知っておきたい。
①も②も計算できるようにしておいたほうがよい。特に今回の例題の関数
![]()
などは ![]() 周りでローラン展開できるようにしておいたほうがよい。
周りでローラン展開できるようにしておいたほうがよい。
2. 例題を解きながら留数定理の準備
なぜローラン展開したか(留数の意味)
一般的な話を簡単にしておく。ローラン展開の前にまず、上の①の積分を具体的に書いてみよう。下図のように![]() 以外の複素積分はすべて 0 になる。
以外の複素積分はすべて 0 になる。
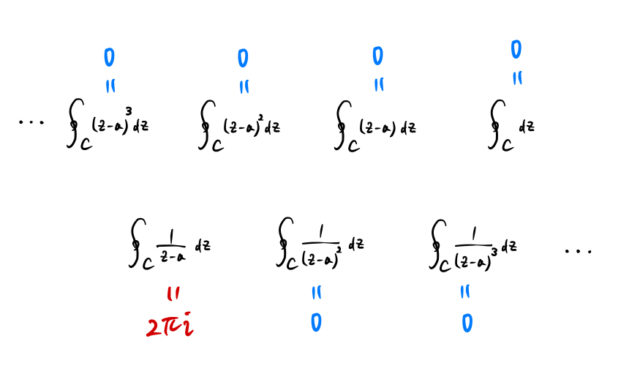
逆に言うと、複素積分すると ![]() の部分は「残り物」として
の部分は「残り物」として ![]() になる。この性質を使うと、複素積分をうまいこと計算できそうな気がするだろう。
になる。この性質を使うと、複素積分をうまいこと計算できそうな気がするだろう。
これを踏まえて、下図のローラン展開の形を見て欲しい。
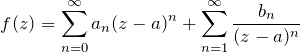
右辺の項ごとの複素積分は簡単に計算できそうである。なぜなら ![]() 以外 0 なのだから!
以外 0 なのだから!
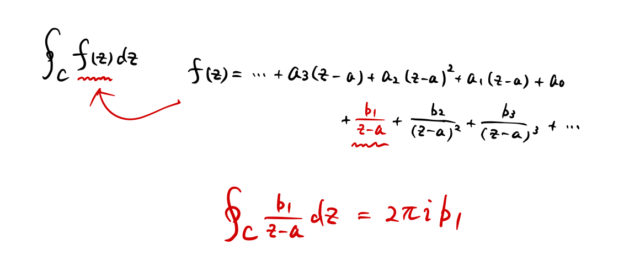
そして 0 でない唯一の「残り物」の係数 ![]() のことを「留数」と呼ぶ。ここでローラン展開したのは、
のことを「留数」と呼ぶ。ここでローラン展開したのは、
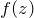 の複素積分を実行するため
の複素積分を実行するため- 留数
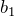 を探すため
を探すため
である。ちなみに、「留数」は英語で residue(残量物)、
「他の部分が取りされた後残ったもの」
(“something left after other parts have been taken away”)(weblioより)
という意味である。留数 ![]() を表すのに
を表すのに ![]() などの表記がある。これ以外の表記もあるので、自分が一番かっこいいと思う記号を使えばいいと思う。
などの表記がある。これ以外の表記もあるので、自分が一番かっこいいと思う記号を使えばいいと思う。
例題の解答
上で見たように ![]() の留数
の留数 ![]() を求めれば複素積分は計算できる。つまり、3ステップで良い。
を求めれば複素積分は計算できる。つまり、3ステップで良い。
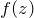 をローラン展開する
をローラン展開する- 留数
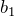 を求める
を求める - 複素積分の値は
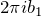
以下では、このステップに沿って計算する。
![]()
を計算する。
1 ローラン展開 (![]() まわり):
まわり):
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(z)=\frac{1}{z(z+1)} &=&\frac{1}{z}\cdot\frac{1}{z+1}\\\\ &=&\frac{1}{z}\left[ 1-z+z^2-z^3+\cdots \right]\\\\ &=& \textcolor{red}{\frac{1}{z}}-1+z-z^2+\cdots \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-bf6eb47565621f74b1b59c49723c4d67_l3.png)
2 留数 ![]() を求める:
を求める:
上の展開の通り、![]() の係数は 1 である。よって
の係数は 1 である。よって
![]()
3 複素積分の値
以上より、
![]()
これで複素積分を計算できた!なぜ ![]() だけでよかったか具体的に見てみよう。
だけでよかったか具体的に見てみよう。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \oint_C \frac{1}{z(z+1)} \, dz &=&\oint_C \left[\frac{1}{z}-1+z-z^2+\cdots\right] \, dz\\\\ &=& \textcolor{red}{\oint_C \frac{1}{z}\, dz} -\cancel{\oint_C \, dz} +\cancel{\oint_C z \, dz} -\cancel{\oint_C z^2\, dz} +\cdots\\\\ &=&2\pi i \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-221a84c7626f7aa1e4738698032e2edc_l3.png)
![]() の部分のみが
の部分のみが ![]() で残るのである。
で残るのである。
n位の極とは?
さっきの関数のローラン展開をわかりやすく書いてみる。
![]()
![]() がなく、
がなく、![]() で特異的な部分は
で特異的な部分は ![]() である。この関数の特異点
である。この関数の特異点 ![]() を1位の極と呼ぶ。つぎに、上の関数を
を1位の極と呼ぶ。つぎに、上の関数を ![]() で割った関数を考える。
で割った関数を考える。
![]()
![]() で特異的な部分は
で特異的な部分は ![]() と
と ![]() である。この新しい関数の特異点
である。この新しい関数の特異点 ![]() を
を ![]() 位の極とよぶ。イメージでいうと、
位の極とよぶ。イメージでいうと、![]() に近づけた時の発散スピードは
に近づけた時の発散スピードは ![]() のほうが早いため、2位の極のほうが「強い」感じであろうか。より高位の極については、
のほうが早いため、2位の極のほうが「強い」感じであろうか。より高位の極については、![]() に対して
に対して ![]() 位の極とよぶだけである。
位の極とよぶだけである。
念の為、![]() の留数は上のローラン展開の形から
の留数は上のローラン展開の形から ![]() になっていることを確認して欲しい。だから、
になっていることを確認して欲しい。だから、
![]()
になる。
3. 留数定理
留数定理(1位の極)
上の例題で確認したように、
![]()
であった。ここで、ローラン展開せずに 留数 ![]() を取り出す方法を考えよう。ローラン展開しないで留数を求めて、複素積分値を計算するのが「留数定理」である。
を取り出す方法を考えよう。ローラン展開しないで留数を求めて、複素積分値を計算するのが「留数定理」である。
1位の極について:
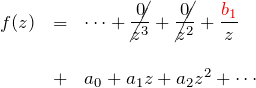
両辺に ![]() をかける:
をかける:
![]()
![]() を特異点に近づける (
を特異点に近づける ( ![]() ):
):
![Rendered by QuickLaTeX.com \begin{eqnarray*} \lim_{z\to 0} zf(z)&=& \lim_{z\to 0}\left[\textcolor{red}{b_1} +a_0 z + a_1 z^2 + a_2 z^3 + \cdots\right]\\\\ &=&\textcolor{red}{b_1} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8e97c30dfe07b99c3ca14d8631a09f74_l3.png)
留数を取り出せた!
![]() が1位の極の場合は、
が1位の極の場合は、![]() まわりのローラン展開から出発する。
まわりのローラン展開から出発する。
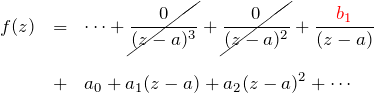
両辺に ![]() をかけて、
をかけて、![]() をとる:
をとる:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \lim_{z\to a}(z-a)f(z)&=& \lim_{z\to a}\left[\textcolor{red}{b_1} +a_0 (z-a) + a_1 (z-a)^2 + a_2 (z-a)^3 + \cdots\right]\\\\ &=&\textcolor{red}{b_1}=Res[a,f] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0ee8f403db9577423f6e45f0171bb3f2_l3.png)
![]() の値がわかったので、これに
の値がわかったので、これに ![]() をかければ複素積分の結果になる。以上の結果をまとめよう。
をかければ複素積分の結果になる。以上の結果をまとめよう。
![]()
つまり、複素積分の結果は ![]() ×(留数)である(特異点が1個のとき)。そして、留数の求め方は、
×(留数)である(特異点が1個のとき)。そして、留数の求め方は、
- ローラン展開して
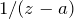 の係数を調べる
の係数を調べる 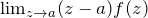 を計算する(1位の極)
を計算する(1位の極)
のどちらかで良い。
留数定理(2位の極)
これは2位を理解すれば、 ![]() 位の極は簡単に求めることができる。
位の極は簡単に求めることができる。
同じくローラン展開から出発する。目的地は留数 ![]() を求めることである。
を求めることである。
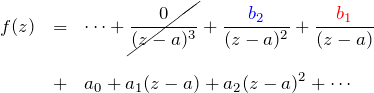
今度は ![]() が生きている。ここで、試しに
が生きている。ここで、試しに ![]() をかけてみる。
をかけてみる。
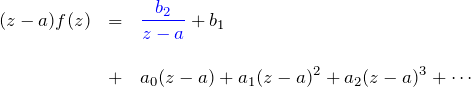
![]() とすると、右辺の第一項(青色部分)で特異的である。これはよくないので、もう一回
とすると、右辺の第一項(青色部分)で特異的である。これはよくないので、もう一回 ![]() をかける。
をかける。
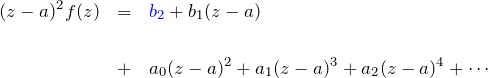
特異的な部分は消えた。しかし、![]() で
で ![]() の項が消えてしまう。これはよくない。
の項が消えてしまう。これはよくない。
ここで両辺を微分する!
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{d}{dz}\left[(z-a)^2 f(z)\right]&=& \cancel{\textcolor{blue}{(b_2)'}}+b_1 \\\\&+&2a_0(z-a) + 3a_1 (z-a)^2 + 4a_2 (z-a)^3 +\cdots \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1816311000e369cb2da7de3adc362c79_l3.png)
これで ![]() を取ってやると、
を取ってやると、
![]()
すばらしい。![]() を求めることができた。これより2位の極の場合の留数定理がわかる。
を求めることができた。これより2位の極の場合の留数定理がわかる。
![]()
留数定理(n位の極)
ここはもう簡単に説明する。![]() に
に ![]() をかけたところから始めよう。
をかけたところから始めよう。
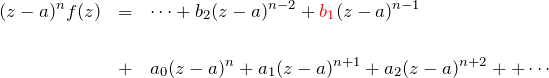
![]() としたときに
としたときに ![]() が残るようにするために、
が残るようにするために、![]() 回微分する。そして、
回微分する。そして、![]() をとる。
をとる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \lim_{z\to a}\frac{d^{n-1}}{dz^{n-1}}\left[(z-a)^n f(z)\right]= (n-1)\cdot(n-2)\cdots 3\cdot 2 \cdot 1 b_1\\\\ \Leftrightarrow b_1=\lim_{z\to a}\frac{1}{(n-1)!}\frac{d^{n-1}}{dz^{n-1}}\left[(z-a)^n f(z)\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-5711ba46d5b3898d83af9c4713916d02_l3.png)
として留数を求めることができた。複素積分は ![]() であるため留数定理が導かれる。
であるため留数定理が導かれる。
![]()
4. まとめ
ローラン展開 → 留数 → 留数定理 と説明した。複素積分を求めたいなら、留数 ![]() を求めて
を求めて ![]() をかければよい。
をかければよい。
留数の求め方は、
- ローラン展開して
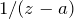 の係数を調べる
の係数を調べる 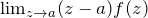 を計算する(1位の極)
を計算する(1位の極)
である。留数定理がわかれば、複素積分の応用問題につまづくことはないだろう。
<脚注(思いついたことを書く場所)>
![]() :数学者ピエール・アルフォンス・ローラン(Pierre Alphonse Laurent) は男性であるため、妖艶という形容詞はちょっと違う。ローラン展開の「妖艶さ」のイメージはイヴ・サンローランから来ている(自分の中で)。そしてフランス語は読みにくい。
:数学者ピエール・アルフォンス・ローラン(Pierre Alphonse Laurent) は男性であるため、妖艶という形容詞はちょっと違う。ローラン展開の「妖艶さ」のイメージはイヴ・サンローランから来ている(自分の中で)。そしてフランス語は読みにくい。