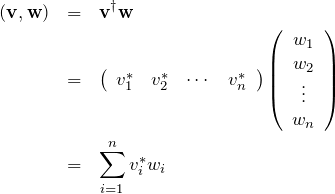行列やベクトルをその ![]() 行、
行、![]() 列成分(
列成分( ![]() 成分)で表すことがある。たとえば、
成分)で表すことがある。たとえば、![]() 行列
行列 ![]() について
について
と書かずに、 ![]() とだけ書く。数式の見かけがすっきりするためよく使われ、いくつかの関係式の証明にも便利である。ここでは、ベクトルや行列を単に成分で書いて、行列の積などについてまとめておく。
とだけ書く。数式の見かけがすっきりするためよく使われ、いくつかの関係式の証明にも便利である。ここでは、ベクトルや行列を単に成分で書いて、行列の積などについてまとめておく。
目次
成分で表示
考えるベクトルの成分 ![]() や行列の成分
や行列の成分 ![]() は複素数
は複素数 ![]() とする。実数の成分を考える場合は複素共役をとるときに注意すれば良い。 *
とする。実数の成分を考える場合は複素共役をとるときに注意すれば良い。 * ![]() など太字はベクトルを表す。
など太字はベクトルを表す。
n次ベクトル
![]() 次の(縦)ベクトルは
次の(縦)ベクトルは
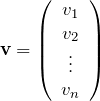
である。このベクトルを
![]()
と略記する。
n×m行列
![]() 行列
行列

について、
![]()
と略記する。
行列を列ベクトルで表示
上の行列は
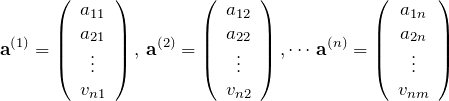
を並べて
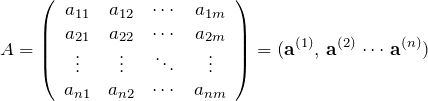
と書ける。これより、
![]()
である(![]() は列ベクトル
は列ベクトル ![]() の
の ![]() 成分)。
成分)。
重要な関係式と成分表示
行列の和の成分
![]() 行列
行列 ![]() に対して、
に対して、![]() もまた
もまた ![]() 行列になる。
行列になる。
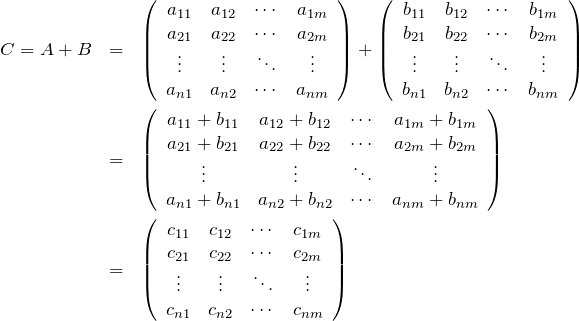
である。これを成分で書くと、
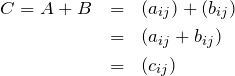
行列の積の成分
![]() 行列
行列 ![]() と
と ![]() 行列
行列 ![]() との積
との積 ![]() を考える。
を考える。![]() は
は ![]() 行列になる。
行列になる。

これより、![]() を具体的に書くと
を具体的に書くと
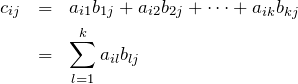

行列の積の形はよく出てくる。とくに ![]() 行列
行列 ![]() の積
の積 ![]() についての以下の形をよく使う。
についての以下の形をよく使う。
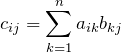
![]() は
は ![]() を取るためのダミーの変数で、
を取るためのダミーの変数で、![]() でも何でも良い。
でも何でも良い。
転置行列
転置行列は、行列の行と列を入れ替えて作る。![]() 行列
行列

の転置行列は
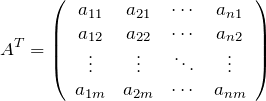
となる。成分で表すと
![]()
行列の積の転置
![]() 行列
行列 ![]() と
と![]() 行列
行列 ![]() の積
の積 ![]() (
(![]() 行列)について転置を取る。このとき、以下が成り立つ。
行列)について転置を取る。このとき、以下が成り立つ。
![]()
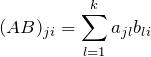
である。よって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Bigl[(AB)^T\Bigr]_{ij}&=& (AB)_{ji}\\ &=&\sum_{l=1}^k a_{jl}b_{li}\\ &=&\sum_{l=1}^k b_{li}a_{jl}\\ &=&\sum_{l=1}^k (B^T)_{il}(A^T)_{lj}\\ &=&(B^T A^T)_{ij}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-3b3ad00baf45fd9155022b866f078836_l3.png)
*
随伴行列(エルミート共役)
![]() の随伴行列
の随伴行列 ![]() (読み:エーダガー)は、
(読み:エーダガー)は、![]() の行列の転置をとり複素共役をとることで作られる。
の行列の転置をとり複素共役をとることで作られる。 ![]() の複素共役をとった後に転置をとっても良い。
の複素共役をとった後に転置をとっても良い。![]() を
を ![]() のエルミート共役とも呼ぶ。
のエルミート共役とも呼ぶ。
つまり、定義:
![]()
具体的に書くと、![]() 行列
行列

の随伴行列は
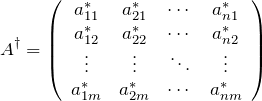
である。成分で書くと、
![]()
とくに ![]() となる、すなわち随伴行列が自分自身に一致する行列のことをエルミート行列と呼ぶ。
となる、すなわち随伴行列が自分自身に一致する行列のことをエルミート行列と呼ぶ。
トレース(跡): TrA
![]() 次正方行列
次正方行列 ![]() に対し、対角成分の和をとることを「行列
に対し、対角成分の和をとることを「行列 ![]() のトレースをとる」と言う。
のトレースをとる」と言う。
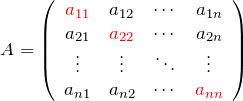
のトレース ![]() は
は
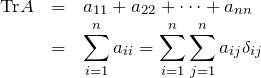
![]() は
は![]() を取るためのダミーで記号は
を取るためのダミーで記号は ![]() などでも良い。
などでも良い。![]() はクロネッカーのデルタで、
はクロネッカーのデルタで、
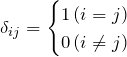
行列の積のトレース: Tr(AB)=Tr(BA)
上で見たように、![]() 行列の
行列の ![]() 積
積 ![]() (
(![]() 行列)について、
行列)について、
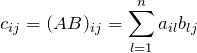
であった。したがって、上の ![]() を参考に
を参考に ![]() として
として
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\rm Tr}C&=&\sum_{i=1}^n c_{ii}=\sum_{i=1}^n \Bigl[\sum_{k=1}^n a_{ik}b_{ki} \Bigr]\\ &=&\sum_{i=1}^n \sum_{j=1}^n a_{ij}b_{ji}\quad(k\to j) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4c3263214609b7dea7a71a5fcb87ca66_l3.png)
これから、![]() がわかる。
がわかる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\rm Tr}(AB)&=& \sum_{i=1}^n \sum_{j=1}^n a_{ij}b_{ji}\\ &=& \sum_{j=1}^n \sum_{i=1}^n b_{ji}a_{ij}\\ &=& \sum_{j=1}^n \Bigl[\sum_{i=1}^n b_{ji}a_{ij}\Bigr]\\ &=& \sum_{j=1}^n (BA)_{jj}\\ &=& {\rm Tr}(BA)\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8aa0742ad70feabd5144c06932751d04_l3.png)
* 積 ![]() は単なる複素数の積なので入れ替えても良い。
は単なる複素数の積なので入れ替えても良い。
ベクトルの内積
![]() 次元列ベクトル
次元列ベクトル ![]() を考える。
を考える。
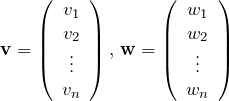
実ベクトルの内積
![]() の成分がすべて実数のときを考える(実ベクトル)。 内積
の成分がすべて実数のときを考える(実ベクトル)。 内積 ![]() は
は
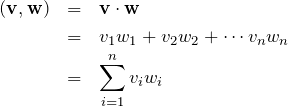
また内積は、行ベクトル ![]() と列ベクトル
と列ベクトル ![]() の積(行列同士の積)でも書ける。行ベクトルは列ベクトルの転置を取ることでできる。
の積(行列同士の積)でも書ける。行ベクトルは列ベクトルの転置を取ることでできる。
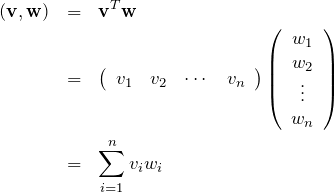
![]() は
は ![]() 行列、
行列、 ![]() は
は ![]() 行列とも考えれる。このとき、
行列とも考えれる。このとき、![]() と
と ![]() は行列として扱うので、行列の内積
は行列として扱うので、行列の内積 ![]() のように
のように ![]() ではない。
ではない。
複素ベクトルの内積
次にベクトルの成分が複素数の場合を考える。このとき、内積は 内積 ![]() は
は
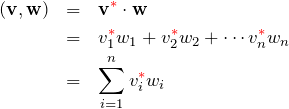
である。また、列ベクトル ![]() を
を ![]() 行列と見たときの随伴行列
行列と見たときの随伴行列 ![]() を用いて
を用いて