以下、実数 ![]() ,
, ![]() 次正方行列
次正方行列 ![]() とする。
とする。![]() と同じように、
と同じように、![]() としたとき
としたとき
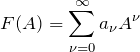
のようにベキ級数展開が定義できる。このとき、行列の積の定義から ![]() は
は ![]() 次正方行列になる。また、これに関連していくつかの重要な性質をまとめる。
次正方行列になる。また、これに関連していくつかの重要な性質をまとめる。
* ここで ![]() は行列なので、
は行列なので、![]() とせずに大文字の
とせずに大文字の ![]() を使っている。
を使っている。
目次
関数の展開
一般に関数 ![]() は
は
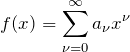
のように多項式でベキ級数展開できる。このことはテイラー展開(マクローリン展開)と同じである。
正方行列Aの関数
上の ![]() と同じように
と同じように ![]() についてもベキ級数が定義できる。
についてもベキ級数が定義できる。
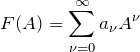
F(P^-1 A P)
逆行列の定義できる ![]() 次正則行列
次正則行列 ![]() を用いて
を用いて
![]()
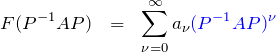
ここで、
![]()
となる。したがって、
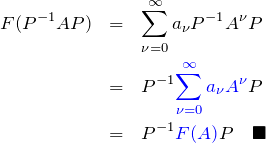
exp(A) (指数関数形)
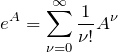
指数関数の展開
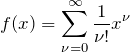
より、
exp(A+B) (AB=BAのとき)
![]() (
(![]() の行列が交換する)とき
の行列が交換する)とき
![]()
左辺は
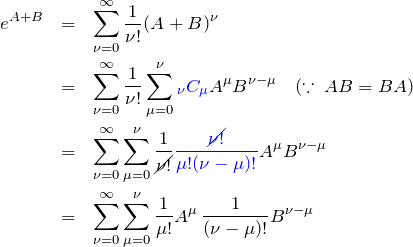
また、右辺は
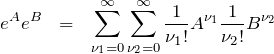
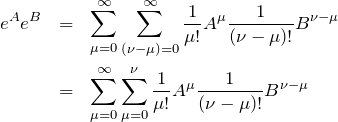
より、
![]()
exp(A) exp(A^-1)
![]()
証明:上の式で、![]() とすればよい。
とすればよい。
F(A)のエルミート随伴: [F(A)]^†
![]()
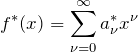
![Rendered by QuickLaTeX.com \begin{eqnarray*} f^*(A^\dagger)&=&\sum_{\nu=0}^\infty a_\nu^* \left(A^\dagger\right)^\nu\\ &=&\sum_{\nu=0}^\infty \left(a_\nu A\right)^\dagger\\ &=& \left[F(A) \right]^\dagger\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2b4085d858c0a2c9f4308258c5695f4a_l3.png)
*
導関数: F(xA)の微分
![]() がベキ級数で表すことができるとき
がベキ級数で表すことができるとき
![]()
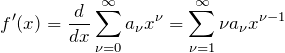
のとき、
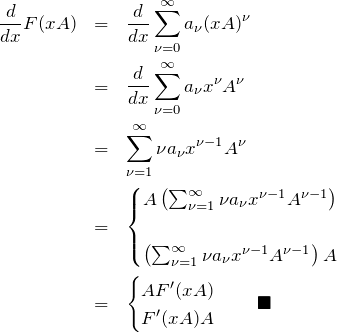
対角行列D
![]() 次正方行列
次正方行列 ![]() の非対角要素が
の非対角要素が ![]() のときを考える。対角行列であることをわかりやすくするため、
のときを考える。対角行列であることをわかりやすくするため、 ![]() を
を ![]() (Diagonal matrix)とする。このとき、
(Diagonal matrix)とする。このとき、![]() 成分を
成分を ![]() とする。
とする。
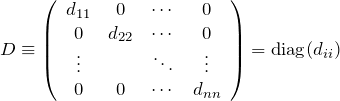
対角行列を ![]() と表すこともある。
と表すこともある。
F(D)=diag(f(dii))
対角行列 ![]() について、
について、![]() は対角的で対角成分は
は対角的で対角成分は ![]() となる。
となる。
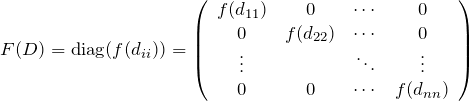
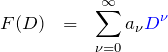
ここで、
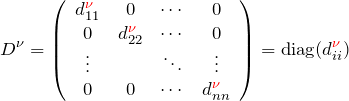
より、行列の対角成分について
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\sum_{\nu=0}^\infty a_\nu D^\nu \right]_{ii}&=& \sum_{\nu=0}^\infty a_\nu d_{ii}^\nu=f(d_{ii}) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-12dead5f11db19c3f0224b72d085701a_l3.png)
これより、
![]()
Aを対角化して使う
![]() の固有値を
の固有値を ![]() 、固有ベクトルを
、固有ベクトルを ![]() (
(![]() 次)とする。このとき、
次)とする。このとき、![]() 次正則行列
次正則行列
![]()
によって ![]() を対角化することができる。これを
を対角化することができる。これを
![]()
と書く(![]() )。このとき、上に示したいくつかの関係式を使って
)。このとき、上に示したいくつかの関係式を使って
![]()
などが成り立つ。たとえば、![]() について
について
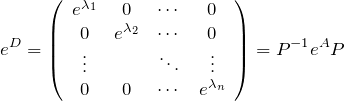
など。