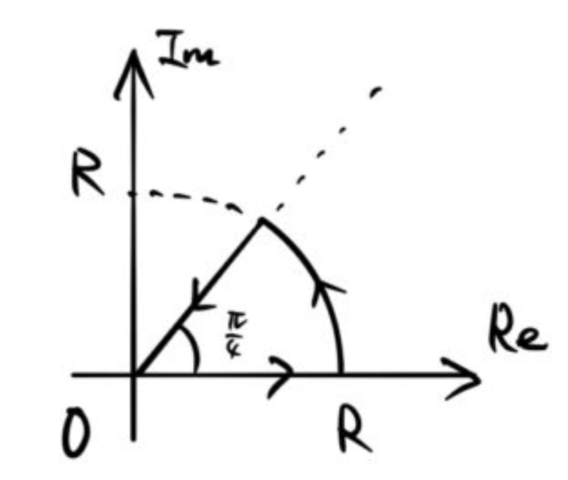
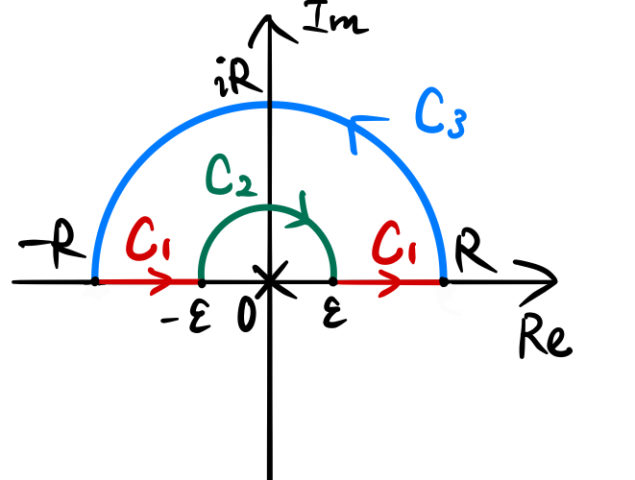
コーシーの積分公式などに関係する計算。これは留数定理にも関係する話。下の式において、積分経路 ![]() 内に
内に ![]() がある場合を考える。積分経路の外に
がある場合を考える。積分経路の外に ![]() がある場合は積分は
がある場合は積分は ![]() になる。
になる。
(z-z0)^n の複素積分
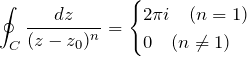
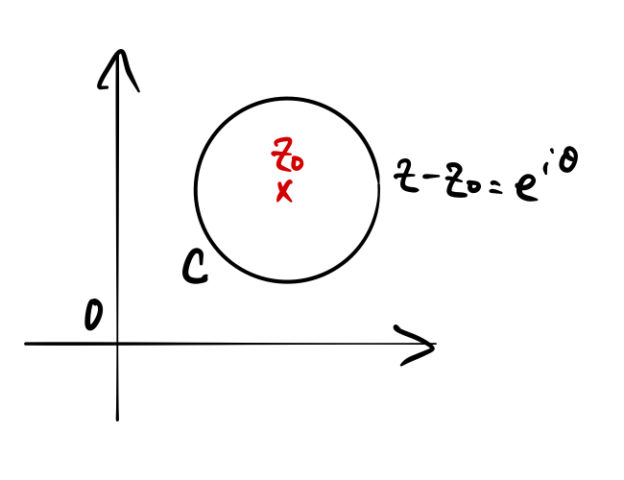
上のように、![]() :
:![]() の単位円として考える。このとき複素積分を具体的に計算したければ、
の単位円として考える。このとき複素積分を具体的に計算したければ、
![]()
と積分変換して計算すれば良い。ここで、
![]()
![]() のとき:
のとき:
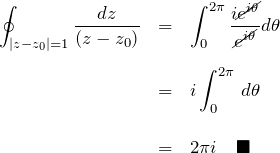
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \oint_{|z-z_0|=1} \frac{dz}{(z-z_0)^n} &=& \int_0^{2\pi} \frac{ie^{i\theta}}{e^{in\theta}}\,d\theta\\\\ &=& i\int_0^{2\pi} e^{-i(n-1)\theta}\, d\theta\\\\ &=& i\left[-\frac{i}{n-1}e^{-i(n-1)\theta}\right]_0^{2\pi}\\\\ &=& -\left\{ e^{-2(n-1)\pi i}-e^0 \right\}\\\\ &=& -\left\{ \left(e^{-2\pi i})^{(n-1)}-e^0 \right\}\\\\ &=& 0 \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-63dc354b20adcb42f2857a234544ace6_l3.png)
以上より、
(z-z0)^n の複素積分
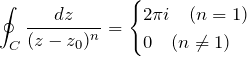
を得る。
これの結果を利用するといくつかの複素積分が実行できる。