フーリエ級数と無限級数和を考える。
例題
![]() で周期的な関数
で周期的な関数
![]()
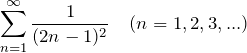
はじめに
![]() で定義された周期
で定義された周期 ![]() 周期関数
周期関数 ![]() は、同じく周期
は、同じく周期 ![]() の三角関数で展開できそうである。
の三角関数で展開できそうである。
![]()
したがって、
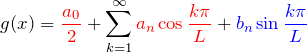
と表す。![]() はフーリエ係数と呼ばれる。三角関数の直交性,
はフーリエ係数と呼ばれる。三角関数の直交性,
フーリエ級数で一番大事な式
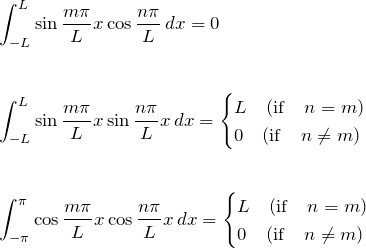
を用いてフーリエ係数は導出できる。
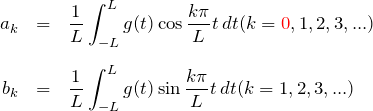
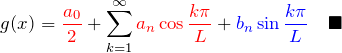
f(t)=|t|のフーリエ係数
![]() で周期 2 の
で周期 2 の ![]() は偶関数である。したがって、フーリエ級数は偶関数のみ残る。つまり、
は偶関数である。したがって、フーリエ級数は偶関数のみ残る。つまり、![]() のシーリズのみで展開できる(
のシーリズのみで展開できる(![]() )。
)。
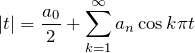
ここで、フーリエ係数 ![]() は
は ![]() と
と ![]() がともに偶関数であることを利用して、
がともに偶関数であることを利用して、
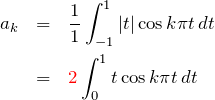
![]() を求める:
を求める:
![]()
![]() を求める:
を求める:
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_0&=&\frac{2}{1}\int_0^{1} t\cos{k\pi t}\, dt\\\\ &=&2\left[ \frac{\cos k\pi t}{(k\pi)^2}+\frac{t\sin k\pi t}{k\pi} \right]_0^{1}\\\\ &=& 2\left\{ \frac{\textcolor{red}{\cos k\pi} - \cos 0}{(k\pi)^2} \right\}\\\\ &=& \frac{2}{k^2\pi^2}\left\{\textcolor{red}{(-1)^k} -1 \right\} \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ef476d6f2ddb40b5e9174a5ba1e07fc7_l3.png)
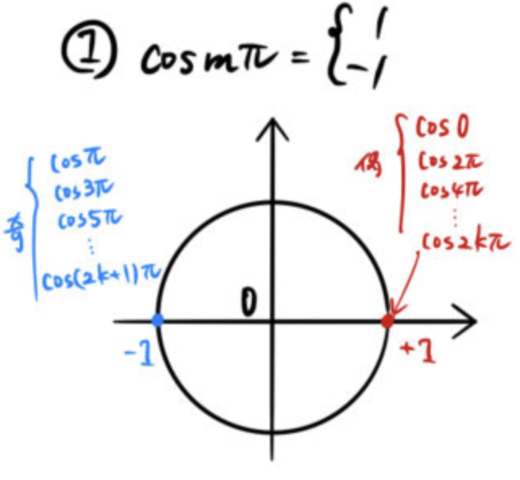
![]() は「フーリエ級数あるある」である(下図)。
は「フーリエ級数あるある」である(下図)。
以上より、![]() をフーリエ級数で表すことができる。
をフーリエ級数で表すことができる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(t)=|t|=\frac{1}{2}+\sum_{k=1}^{\infty}\frac{2}{k^2\pi^2} \left[(-1)^k-1\right]\cos k\pi t\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-d824f411ee769cf467fac46c6ef965af_l3.png)
無限級数を求める
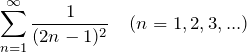
とフーリエ級数の結果を比べて、![]() とおけば良さそうである。
とおけば良さそうである。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&f(0)=0=\frac{1}{2}+\sum_{n=1}^{\infty}\frac{2}{(2n-1)^2\pi^2} \left[(-1)^{2n-1}-1\right]\cos k\pi t\quad\blacksquare\\\\ \Leftrightarrow&&0=\frac{1}{2}+\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \frac{2}{\pi^2}\left[-1-1\right]\\\\ \Leftrightarrow&& -\frac{1}{2}=\frac{2}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2}\cdot(-2) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9b5bd2b315823ae9a8c1471a275b91ea_l3.png)
したがって、
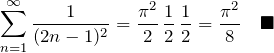
このように、フーリエ級数を利用して無限級数和を表すことができる。