例題として、以下の3問を見ていく。ローラン展開→複素積分の流れで計算した。したがって、複素積分の計算に「留数定理」は使わなかった。参考:「例題で学ぶ:ローラン展開/極/留数定理」 (読了目安:30分)
例題
Cを|z|=1上を反時計回りに一周する積分経路とする。以下の積分を求めよ。
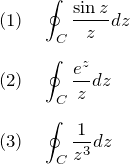
1. 方針
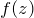 を
を 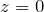 周りで ローラン展開/テイラー展開 する(級数展開)
周りで ローラン展開/テイラー展開 する(級数展開)- 各級数
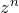 の複素積分において、以下の結果を利用( 導出 )
の複素積分において、以下の結果を利用( 導出 )
1/z^n の複素積分
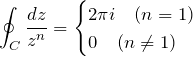
2. 解答
(1) f(z)=sin(z)/z
この関数の特異点は ![]() である。
である。
![]() 中心にローラン展開:
中心にローラン展開:
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(z)&=&\frac{1}{z}\sin z\\\\ &=&\frac{1}{z}\left[ z-\frac{z^3}{3!}+\frac{z^5}{5!}+\cdots \right]\\\ &=& 1-\frac{z^2}{3!}+\frac{z^4}{5!}+\cdots \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8545d6e72912bf99e40dd83c80d5b191_l3.png)
となる。この場合、![]() は除去可能な特異点である。よって、
は除去可能な特異点である。よって、![]() の極はない。言い換えると、留数 (
の極はない。言い換えると、留数 (![]() の係数)がゼロ。したがって、
の係数)がゼロ。したがって、
![]()
あるいは、![]() をローラン展開した各項について
をローラン展開した各項について
![]()
であることを利用しても良い(「1. 方針」参考)。
(2) f(z)=exp(z)/z
この関数の特異点は ![]() である。
である。
![]() 中心にローラン展開:
中心にローラン展開:
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(z)&=&\frac{1}{z}e^{z}\\\\ &=& \frac{1}{z}\left[1+z+\frac{1}{2!}z^2+\frac{1}{3!}z^3+\cdots\right]\\\\ &=& \textcolor{red}{\frac{1}{z}}+1+\frac{1}{2!}z+\frac{1}{3!}z^2+\cdots \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1e89cfd8d0cfb1a179640a642daee4ba_l3.png)
となる。したがって、1位の極をもつ。留数は ![]() の係数である 1 である。留数定理より、
の係数である 1 である。留数定理より、
![]()
あるいは、![]() をローラン展開した結果と
をローラン展開した結果と
![]()
を利用して直接積分しても同じ結果を得る。
(3) f(z)=1/z^3
1/z^nの複素積分と同じである。答えは 0 になる。![]()
![]()
は特異点 ![]() をもつ。これは3位の極である。留数は 0 である。これは
をもつ。これは3位の極である。留数は 0 である。これは ![]() をローラン展開して
をローラン展開して ![]() の係数を見ればわかる。
の係数を見ればわかる。
![]() の
の ![]() まわりのローラン展開:
まわりのローラン展開:
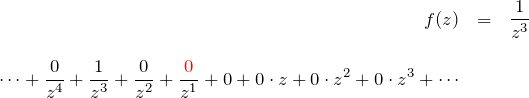
より留数は ![]() である!したがって、留数定理より
である!したがって、留数定理より
![]()
あるいは、
![]()
としてもよい。
3. まとめ
ローラン展開→複素積分を求めてきた。あるいは留数定理でも求めることができる。好きなやり方でやるのがよい。ただ、留数定理を使いすぎると、![]() がどっからきた?ってなるかもしれない。
がどっからきた?ってなるかもしれない。