原点に対して空間反転の操作を行えば、![]() にあった座標は
にあった座標は ![]() へ移される(原点について点対称)。 これは量子力学などの物理ではパリティ変換(反転)として知られ、空間座標の符号を変換する。
へ移される(原点について点対称)。 これは量子力学などの物理ではパリティ変換(反転)として知られ、空間座標の符号を変換する。
たとえば、原子に一様な電場をかけた場合にエネルギー準位が分裂する(シュタルク効果)を考える際にもこの対称性は使われる。
空間反転
直交座標と極座標の場合について見ていく。
直交座標の成分
空間反転により ![]() と変換される。
と変換される。![]() を直交座標系で書くと、空間反転の操作
を直交座標系で書くと、空間反転の操作 ![]() により
により
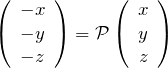
に移される。この操作 ![]() を3
を3![]() 3の行列で表現すれば
3の行列で表現すれば
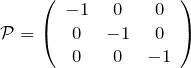
である。![]() となる。通常の軸周りの回転を表す行列
となる。通常の軸周りの回転を表す行列 ![]() ,
, ![]() ,
, ![]() を組み合わせて
を組み合わせて ![]() を作ることはできない。なぜなら、
を作ることはできない。なぜなら、
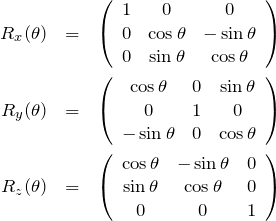
は ![]() であるためである。たとえば、直交行列に関して行列式の性質から
であるためである。たとえば、直交行列に関して行列式の性質から
![]()
となる。
極座標の成分
![]() を極座標表示で表すと
を極座標表示で表すと
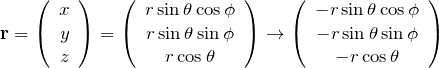
この式から ![]() がどのように変換されるか見ていく。そのあとで、図を書いて
がどのように変換されるか見ていく。そのあとで、図を書いて ![]() の関係を見ていく。
の関係を見ていく。
空間反転に対してベクトルの大きさ変化しない (![]() ) ので
) ので ![]() である。次に
である。次に ![]() について見てみると、
について見てみると、![]() 成分について
成分について ![]() でないといけない。
でないといけない。![]() は変化しないので、
は変化しないので、
![]()
である。したがって、![]() と変換される。最後に
と変換される。最後に ![]() について見ていく。
について見ていく。![]() 成分が
成分が ![]() となるためには、
となるためには、
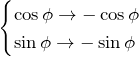
でなくてはならない。したがって、![]() となる。
となる。
これらの結果をまとめると極座標について
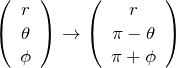
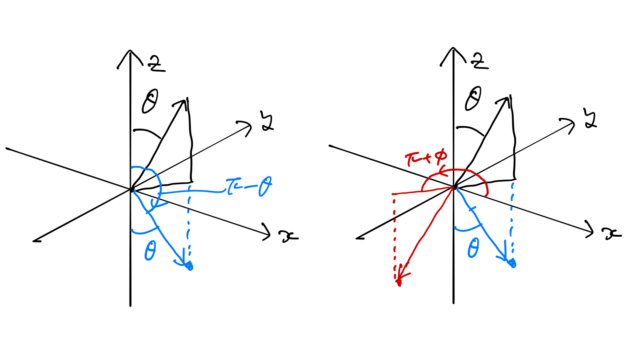
となる。このことを下の図に表した。まず、![]() 平面に対して反転操作を行い(左図)、
平面に対して反転操作を行い(左図)、![]() 軸に対して反時計回りに
軸に対して反時計回りに ![]() 回転すれば(右図)、空間反転に対応することが確認できる。この操作はその性質上、
回転すれば(右図)、空間反転に対応することが確認できる。この操作はその性質上、 ![]() 軸回転から始めて、
軸回転から始めて、![]() 平面の反転をとっても同様の結果になる。
平面の反転をとっても同様の結果になる。
パリティ
以下ではパリティ反転(空間座標を反転させる操作)を表す演算子を ![]() とする。つまり、ある関数
とする。つまり、ある関数 ![]() に対して
に対して
![]()
となる演算子 ![]() について考える。
について考える。
* 式(1)は固有値方程式ではない。固有値方程式は ![]() の形で、両辺に現れる関数は同じ形でないといけない。以下では、
の形で、両辺に現れる関数は同じ形でないといけない。以下では、![]() の固有値・固有関数を考える。
の固有値・固有関数を考える。
固有値・固有関数
![]() の固有値
の固有値 ![]() を考える。固有関数を
を考える。固有関数を ![]() とすると
とすると
![]()
である。両辺にさらに ![]() を左から作用させて、
を左から作用させて、
![]()
式(1)より ![]() を用いると、左辺は
を用いると、左辺は
![]()
となる。したがって、![]() から
から ![]() となる。固有値
となる。固有値 ![]() に対して固有関数
に対して固有関数 ![]() と書くと、
と書くと、
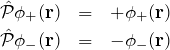
一方、式(1)より ![]() の関係を用いて左辺を書き直すと
の関係を用いて左辺を書き直すと
![]()
これより、![]() は偶関数(パリティが偶)、
は偶関数(パリティが偶)、![]() は奇関数(パリティが奇)となる。任意の関数はこの2つの
は奇関数(パリティが奇)となる。任意の関数はこの2つの ![]() で展開することができ、完全系をなす。
で展開することができ、完全系をなす。
水素原子のハミルトニアンとの交換関係
水素原子のシュレディンガー方程式について、電子の受けるポテンシャルは原子からのクーロンポテンシャルのみで球対称になっている。したがって、ポテンシャルは ![]() の関数であり、角度によらないポテンシャルになる。
の関数であり、角度によらないポテンシャルになる。
直交座標系で書いたハミルトニアンは、
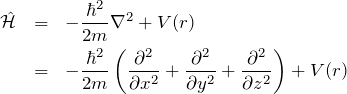
となる。ここで、空間反転 ![]() について球対称ポテンシャルは以下のように形を変えない。
について球対称ポテンシャルは以下のように形を変えない。
![]()
また、![]() などの部分について、
などの部分について、
![]()
より、空間反転に対して不変である。したがって、上の ![]() は空間反転に対して不変である。極座標表示したハミルトニアンでも同様の結果になる。ハミルトニアンが空間反転に対して不変であるので、交換関係は
は空間反転に対して不変である。極座標表示したハミルトニアンでも同様の結果になる。ハミルトニアンが空間反転に対して不変であるので、交換関係は
![]()
となる。
まず
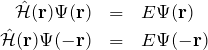
である。また、
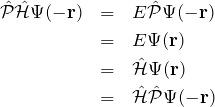
となり、
![]() が交換するため
が交換するため ![]() と
と ![]() は同時固有状態をもつ。
は同時固有状態をもつ。![]() の固有状態は、水素原子における電子の波動関数
の固有状態は、水素原子における電子の波動関数 ![]() であり、動径波動関数
であり、動径波動関数 ![]() と球面調和関数
と球面調和関数 ![]() の積で表されていた。したがって、
の積で表されていた。したがって、![]() の固有関数である
の固有関数である ![]() は
は ![]() の固有関数でもある(同時固有状態)。よって
の固有関数でもある(同時固有状態)。よって
![]()
となる。波動関数のパリティ(![]() が偶関数か奇関数か)によって固有値
が偶関数か奇関数か)によって固有値 ![]() が異なる。あとで示されるように
が異なる。あとで示されるように ![]() であり、パリティは量子数
であり、パリティは量子数 ![]() のみ依存することがわかる。
のみ依存することがわかる。
![]()
![]() に対応する
に対応する ![]() 軌道、
軌道、![]() 軌道、
軌道、![]() 軌道はそれぞれ同じ
軌道はそれぞれ同じ ![]() で指定される球面調和関数
で指定される球面調和関数 ![]() の線形結合で表される。したがって、上のパリティはそのまま、
の線形結合で表される。したがって、上のパリティはそのまま、![]() 軌道のパリティに対応する。たとえば、
軌道のパリティに対応する。たとえば、![]() の
の ![]() 軌道,
軌道, ![]() 軌道に対しては偶パリティで、
軌道に対しては偶パリティで、![]() の
の ![]() 軌道,
軌道, ![]() 軌道は奇パリティである。
軌道は奇パリティである。
球面調和関数のパリティ
最後に、![]() となることを示す。
となることを示す。![]() の空間反転において、
の空間反転において、![]() より動径関数
より動径関数 ![]() は偶関数となる。これより
は偶関数となる。これより
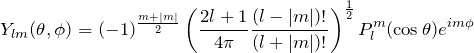
について ![]() に対する偶奇を調べる。まず、
に対する偶奇を調べる。まず、
![]()
となる。次にルジャンドル陪多項式 ![]() について考える。ルジャンドル多項式
について考える。ルジャンドル多項式 ![]() はロドリゲスの公式より
はロドリゲスの公式より
![]()
と書ける。![]() を用いて
を用いて ![]() は
は
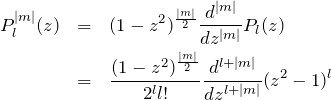
となる。![]() に対して、
に対して、
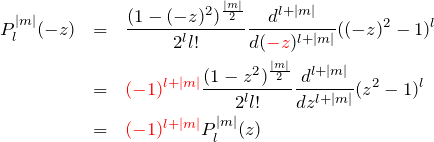
となる。この結果と(2)より ![]() は
は ![]() に対して
に対して
![]()
となる。これより
![]()