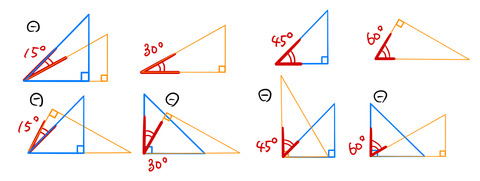
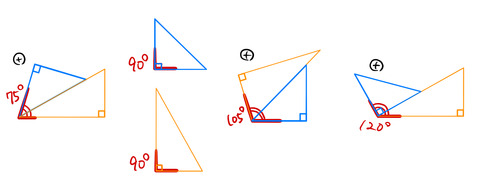
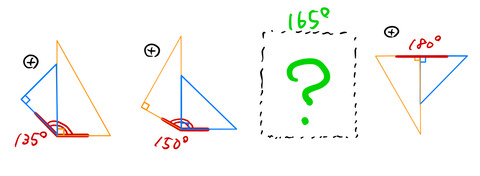【三角定規】165度をつくり、整数問題として遊ぶ

　２つの三角定規を組み合わせてでいろいろな角度をつくる。どんな角度が作れて、どんな角度がつくれないかを調べる。具体的にいろいろ作ってみた。そして整数に置き換えて考えてみたり、もっと多くの三角定規でもっと多くの組み合わせを考えてみたい。

1. 2個の定規で遊ぶ
2. 165度を作る
- 2.1 外角を使う
- 2.2 3個の定規使う
3. 簡単な整数にして遊ぶ
4. 4個以上の定規を使っちゃう
5. まとめ

1. 2個の定規で遊ぶ

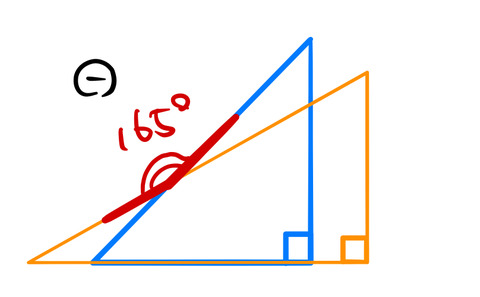
“＋”：角度の和で作った角度
“ー”：角度の差で作った角度

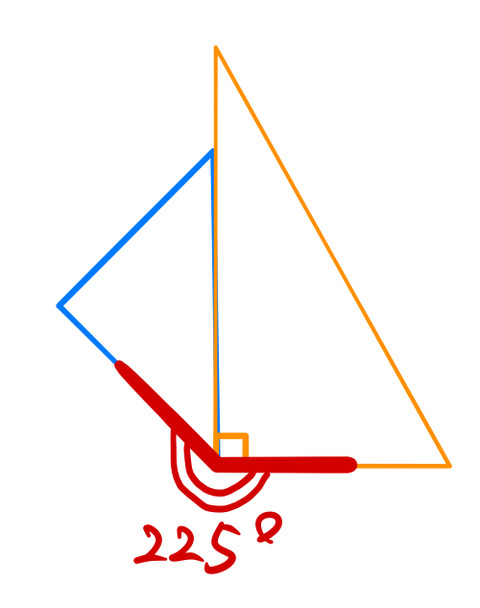
を表す。１５度刻みで様々な角度をつくることができた。１８０度以上の角度は、１８０度以下の角度で表すことができる。例えば、２２５度の場合は、（３６０ー２２５）度＝１３５度を用いて図のように作られる。

本当に１６５度は作れないのだろうか。

否、作れる。

2. 165度を作る

　結論から述べると１６５度を作るためには、

「外角」を使う
３個の３角定規を使う

必要がある。

2.1 外角を使う

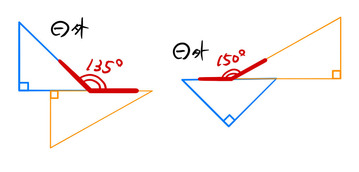
　ここまでは和と差で角度を作ってきた。しかし、「外角」の概念を使えばもっと自由に角度を作ることができる。したがって、１６５度＝（１８０ー１５）度をつくるためには、１５度の外角を利用すればいい。つまり、下図のようにすれば良い。

外角を使えば、１３５度や１５０度も４５度や３０度で表すことができる。

2.2 3個の定規使う

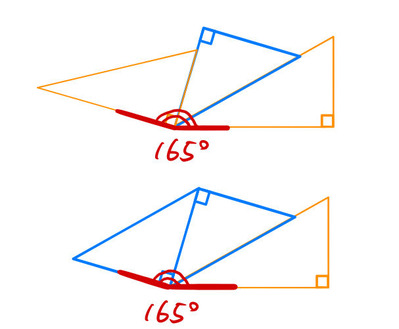
　この方法では、外角は不要である。３個の定規を使えることで表現の自由度が増えた。１６５度については下のように作れる。

　以上のように「外角」を使うか、３個の三角定規を使えば、０から１５度刻みで３６０度まで表すことができる。

3. 簡単な整数にして遊ぶ

　ここからはお遊びである。上記の三角定規の問題をシンプルな整数問題としてみよう。三角定規の角度は 30度、45度、60度、90度ですべて15の倍数である。ここでは、三角定規の角度を簡単な整数に置き換える。つまり、
[30, 60, 90] —> [2, 4, 6]
[45, 45, 90] —> [3, 3, 6]
と簡略化して、整数問題（というほど高級でもない）に帰着する。

２つの三角定規の場合（外角は使わない）
問題は、
“[0,2,4,6] と [0,3,6] ([3,3,6]) から数字を１つずつ選び和か差をとって、１から１２までの整数を作り方”
を求めることである。作り方の組み合わせは表のようになる（”０”は三角定規を使わないを意味する。）。

求める整数
1	3	ー	2
1	3	ー	4
2	0	＋	2
2	6	ー	4
3	3	＋	0
3	6	ー	3
4	0	＋	4
4	6	ー	2
5	3	＋	2
6	0	＋	6
6	6	＋	0
7	3	＋	4
8	6	＋	2
9	3	＋	6
10	6	＋	4
11
12	6	＋	6

漏れがあるといけないのでPythonコードを用いて計算してもらった。どう頑張っても外角なしでは鬼門である１６５度に対応する１１はつくれない。１１以外の１６個について対応する三角形は、この記事の一番初めに示した図に載せている。

３つの三角定規の場合（外角、差は使わない）

使う定規は、上記の２つの定規に[30, 60, 90] の定規か[45, 45, 90]の定規を追加した以下の、
[30, 60, 90] —> [2, 4, 6]
[45, 45, 90] —> [3, 3, 6]
[30, 60, 90] or [45, 45, 90] —> [2,3,4,6]
を考える。差を使うと組み合わせが多くなるため、単に和のみで表現できるものを考える。[2,3,4,6] はUNOでいうワイルドカードである。ドロー4があればとこの問題にゲーム性が出る。

問題は、
“[2,4,6] 、[3,6]、 [2,3,4,6] から数字を１つずつ選び和をとって、１から１２までの整数を作り方”
を求めることである。

“０”（定規を使わない）を入れると、２個の定規の表と同じ組み合わせのものができるため、”０”は考えない。３つの和の場合も機械が計算してくれた。できた表は下の通りである。

求める整数
7	3	＋	2	＋	2
8	3	＋	2	＋	3
9	3	＋	2	＋	4
10	3	＋	4	＋	3
10	6	＋	2	＋	2
11	3	＋	4	＋	4
11	3	＋	6	＋	2
12	3	＋	6	＋	3
12	6	＋	2	＋	4

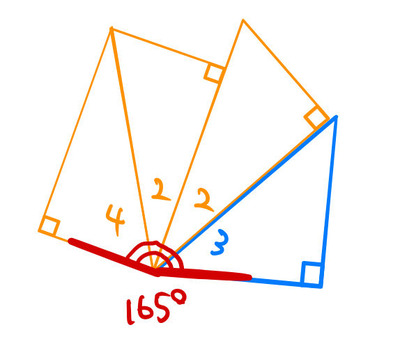
上述したとおり、３つの定規があれば、鬼門であった１６５度に対応する１１についても作ることができる。結局、

$\begin{eqnarray*}165&=&11\times15\\&=&(2+3+6)\times15\\&=&30+45+90\end{eqnarray*}$

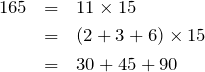
あるいは

$\begin{eqnarray*}165&=&11\times15\\&=&(3+4+4)\times15\\&=&45+60+60\end{eqnarray*}$

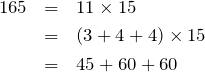
で作れる。この２つは先ほど示した以下のパターンである。

３つの定規の場合の表を見れば、１５０度なども３つの定規を組み合わせて作れることが確認できる。いろいろ試してみてほしい。

4. 4個以上の定規を使っちゃう

　最後に４つ以上の定規を使った場合を計算してみた。結果は以下の通り。

求める整数
9	3	＋	2	＋	2	＋	2
10	3	＋	2	＋	2	＋	3
11	3	＋	2	＋	2	＋	4
11	3	＋	2	＋	3	＋	3
12	3	＋	2	＋	3	＋	4
12	6	＋	2	＋	2	＋	2
11	3	＋	2	＋	2	＋	2	＋	2
12	3	＋	2	＋	2	＋	2	＋	3
12	2	＋	2	＋	2	＋	2	＋	2	＋	3

４つの定規を使った165度の表現（11=3+2+2+4）を下図に示す。

5. まとめ

　これ以上定規を増やしても、机が散らかるだけである。１８０度以上を作ることを考えたらもっと大変になる。

お読みいただきありがとうございました。