ランジュバン関数の導出時には原子の磁気モーメントはあらゆる方向 ![]() を向いていた。ブリルアン関数を導出するときは、量子化されて飛び飛びの値をとる全角運動量
を向いていた。ブリルアン関数を導出するときは、量子化されて飛び飛びの値をとる全角運動量 ![]() による磁気モーメントを考える。
による磁気モーメントを考える。
- ランジュバン関数 ← あらゆる方向の磁気モーメント
- ブリルアン関数 ← 量子化された磁気モーメント
以下の説明において、Feなどの![]() 遷移金属の場合は軌道角運動量の消失により
遷移金属の場合は軌道角運動量の消失により![]() を全スピン角運動量
を全スピン角運動量 ![]() で置き換えて良い。
で置き換えて良い。
1. 基礎知識
ブリルアン関数導出のための基礎知識は以下の通り。
2. ブリルアン関数の導出
仮定:
- 相互作用のない孤立磁気モーメントの集団
- それぞれの原子は一定の磁気モーメント
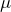 をもつ
をもつ 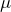 の方向は角運動量
の方向は角運動量 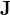 によって量子化
によって量子化- 磁気モーメントを
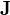 で表す:
で表す: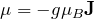
![]() の孤立磁気モーメントの集団に、外部から
の孤立磁気モーメントの集団に、外部から ![]() 方向に磁場
方向に磁場 ![]() をかける。このとき、外部の磁場ベクトルと磁気モーメントのベクトルとの相互作用(エネルギー)は、
をかける。このとき、外部の磁場ベクトルと磁気モーメントのベクトルとの相互作用(エネルギー)は、
![]()
となる。![]() はランデの
はランデの ![]() 因子、
因子、![]() はボーア磁子、
はボーア磁子、![]() は
は ![]() の
の ![]() 成分。
成分。
統計力学ではエネルギー ![]() をもつ状態にある確率は、以下のボルツマン因子に比例する。
をもつ状態にある確率は、以下のボルツマン因子に比例する。
![]()
これは相対確率であり、確率の規格化のため分配関数 ![]() で割る必要がある。つまり取りうるすべての
で割る必要がある。つまり取りうるすべての ![]() についての確率を総和したもので割る。ここで、
についての確率を総和したもので割る。ここで、![]() は
は
![]()
の ![]() 個あるため、
個あるため、![]() の状態を取りうる確率は
の状態を取りうる確率は
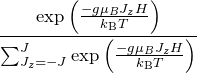
となる。考えている原子数を ![]() とすると、
とすると、![]() 方向の磁気モーメントの大きさ
方向の磁気モーメントの大きさ ![]() は
は ![]() の期待値、
の期待値、
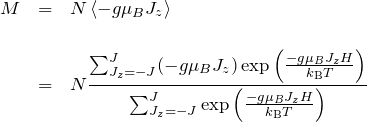
となる。ここで、![]() とおく。
とおく。
分母:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sum_{J_z=-J}^{J} \exp{\left(\frac{-x J_z}{J}\right)} &=& \sum_{J'=0}^{2J}\exp{\left(\frac{-x (J'-J)}{J}\right)}\quad(J'\equiv J_z+J) \\\\ &=& \exp{\left( x \right)}\sum_{J'=0}^{2J}\exp{\left(\frac{-x J'}{J}\right)}\\\\ &\textcolor{blue}{=}& \exp{\left( x \right)}\cdot 1\cdot \frac{1-\exp{\left(\frac{-x (2J+1)}{J}\right)}}{1-\exp{\left(\frac{-x }{J}\right)}}\\\\ &=& \left(1-\exp{\left(\frac{-x (2J+1)}{J}\right)}\right)\cdot \frac{\exp{\left(x\right)}}{1-\exp{\left(-\frac{x}{J}\right)}}\\\\ &=& \frac{1-\exp{\left(\frac{-x (2J+1)}{J}\right)}}{\textcolor{red}{\exp{\left(\frac{-x (2J+1)}{2J}\right)}}} \cdot \frac{\textcolor{red}{\exp{\left(\frac{-x (2J+1)}{2J}\right)}}\exp{(x)}}{1-\exp{\left(-\frac{x}{J}\right)}}\\\\ &=& \left[\exp{\left(\frac{+x (2J+1)}{2J}\right)}-\exp{\left(\frac{-x (2J+1)}{2J}\right)}\right]\cdot \frac{\textcolor{red}{\exp{\left(-x-\frac{x}{2J}\right)}}\exp{(x)}}{1-\exp{\left(-\frac{x}{J}\right)}}\\\\ &=& 2\sinh{\left(\frac{2J+1}{2J}x\right)}\cdot \frac{\exp{\left(-\frac{x}{2J}\right)}}{1-\exp{-\left(\frac{x}{J}\right)}}\\\\ &=& 2\sinh{\left(\frac{2J+1}{2J}x\right)}\cdot \left( \exp{\left(+\frac{x}{2J} \right)} -\exp{\left(-\frac{x}{2J} \right)}\right)^{-1}\\\\ &=& \frac{\sinh{\left(\frac{2J+1}{2J}x\right)}}{\sinh{\left(\frac{x}{2J}\right)}} \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-77f22d5fc962a12587337a41a6107259_l3.png)
3つ目の![]() は等比数列の和の公式:
は等比数列の和の公式:
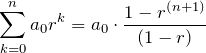
について、公比 ![]() である。また、
である。また、
![]()
である。赤色で強調されている部分は ![]() を作るための変形である。
を作るための変形である。
分子 :
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sum_{J_z=-J}^{J} (- g\mu_B J_z) \exp{\left(\frac{-g\mu_B J_z H}{k_{\rm B}T}\right)} &=&g\mu_B\sum_{J_z=-J}^{J}- J_z \exp{\left(-\frac{xJ_z}{J}\right)}\\\\\\ &=& g\mu_B\cdot J\frac{d}{dx}\left[ \textcolor{red}{ \sum_{J_z=-J}^{J} \exp{\left(-\frac{xJ_z}{J}\right)}} \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2bfeadb3aece9ad9e1966777b23eca08_l3.png)
である。
したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} M&=&Ng\mu_B J\frac{d}{dx}\ln{\left[ \textcolor{red}{\sum_{J_z=-J}^{J} \exp{\left(-\frac{xJ_z}{J}\right)} }\right]}\\\\\\ &=& Ng\mu_B J\frac{d}{dx}\ln{\left[ \textcolor{red}{ \frac{\sinh{\left(\frac{2J+1}{2J}x\right)}}{\sinh{\left(\frac{x}{2J}\right)}} }\right]}\\\\\\ &=& Ng\mu_B J\left\{ \frac{d}{dx}\ln{\left[ \sinh{\left(\frac{2J+1}{2J}x\right)}}\right]} -\frac{d}{dx}\ln{\left[ \sinh{\left(\frac{x}{2J}\right)} }\right] \right\}\\\\\\ &=& Ng\mu_B J\left[ \frac{2J+1}{2J}\coth{\left(\frac{2J+1}{2J}x\right)}} - \frac{1}{2J}\coth{\left(\frac{x}{2J}\right)} \right]\\\\\\ &=& Ng\mu_B J B_J(x) \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8c54d40eb626994901ec8c2eb60edeb8_l3.png)
![]() である。また、最後の行で ブリルアン関数
である。また、最後の行で ブリルアン関数 ![]() を定義した。
を定義した。
![]()
![]() は、磁気モーメントの値が連続だと仮定するランジュバン関数に一致する。
は、磁気モーメントの値が連続だと仮定するランジュバン関数に一致する。
また、 ![]() が小さい時、
が小さい時、
![]()
と展開できる。このとき、
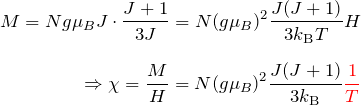
で、帯磁率が温度の逆数に比例する Curieの法則を得る。
3. まとめ
![]() は全角運動量であるが、軌道角運動量
は全角運動量であるが、軌道角運動量 ![]() が無視できる場合は、
が無視できる場合は、![]() として良い。このとき、
として良い。このとき、![]() となる。
となる。
ランジュバン関数より計算は大変である。