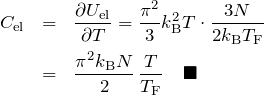低温で、固体中の格子比熱は ![]() の振る舞いをすることがわかっているが、どうも実測値からずれてしまう。 その理由は、低温においては
の振る舞いをすることがわかっているが、どうも実測値からずれてしまう。 その理由は、低温においては ![]() の振る舞いをする電子の比熱が重要であったからだ。 ここではその電子比熱の式を自由電子の状態密度から求めていく。
の振る舞いをする電子の比熱が重要であったからだ。 ここではその電子比熱の式を自由電子の状態密度から求めていく。
前提知識
ゾンマーフェルト展開
ゾンマーフェルト展開は以下で与えられる。
![]()
ここで、
![]()
電子比熱を求める
比熱は温度に対してどれくらいエネルギーが増減するかを表す。 そのため、比熱を求めるためには内部エネルギーの温度依存性を求める必要がある。
内部エネルギー
伝導電子の内部エネルギーへの寄与を求める。
まず電子はおのおのエネルギー ![]() を持っているため、エネルギーの小さい順に並べておく。 下図のように、
を持っているため、エネルギーの小さい順に並べておく。 下図のように、![]() 番目のエネルギー
番目のエネルギー ![]() について、とりうる状態の数は
について、とりうる状態の数は ![]() 個であるとする。 このうち、電子が占有している状態の数は、フェルミ分布関数
個であるとする。 このうち、電子が占有している状態の数は、フェルミ分布関数 ![]() をかけることによって
をかけることによって ![]() となる。
となる。
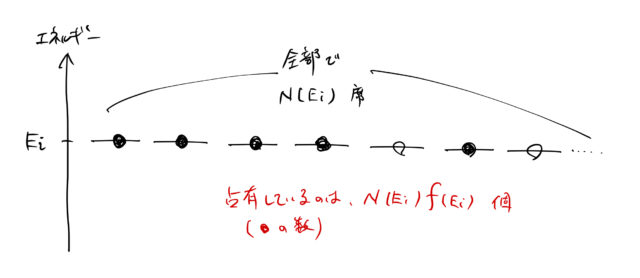
したがって、![]() にある電子のエネルギーの総和は
にある電子のエネルギーの総和は
![]()
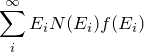
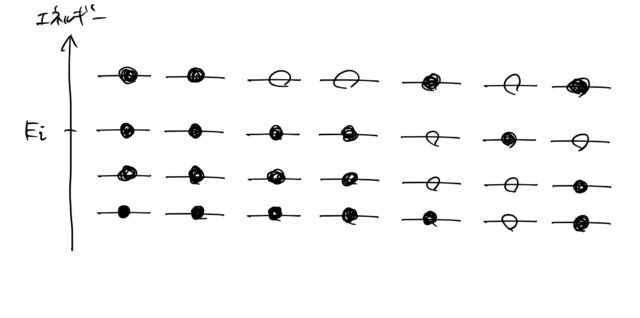
この図はエネルギーが離散的だが、フェルミレベル ![]() あたりまで考えると、ほとんどエネルギーが連続であるかのように扱える。 したがって、離散和
あたりまで考えると、ほとんどエネルギーが連続であるかのように扱える。 したがって、離散和 ![]() を積分に置き換えると、内部エネルギーの電子からの寄与
を積分に置き換えると、内部エネルギーの電子からの寄与 ![]() は
は
![]()
となる。ここで、![]() は状態密度であり、
は状態密度であり、![]() である。 また、フェルミ分布関数は
である。 また、フェルミ分布関数は ![]() を満たす。
を満たす。
温度の効果は ![]() を含むフェルミ分布関数
を含むフェルミ分布関数 ![]() を通して考慮されている。
を通して考慮されている。 ![]() はフェルミレベル
はフェルミレベル ![]() 近傍の「ぼやけ」となってあらわれるため、
近傍の「ぼやけ」となってあらわれるため、![]() まわりで展開する。すなわち、
まわりで展開する。すなわち、![]() としてゾンマーフェルト展開をおこなうと
としてゾンマーフェルト展開をおこなうと
![Rendered by QuickLaTeX.com \begin{eqnarray*} U_{\rm el}&=& \int_{-\infty}^{E_{\rm F}(T)} E'D(E')\,dE' + \frac{\pi^2}{6}(k_{\rm B}T) \frac{d(ED(E))}{dE}\big|_{E=E_{\rm F}(T)}+\cdots\\ &=& \int_{-\infty}^{E_{\rm F}(T)} E'D(E')\,dE' +\frac{\pi^2}{6}(k_{\rm B}T) \Bigg[ D(E_{\rm F}(T)) +E\frac{dD(E)}{dE}\big|_{E=E_{\rm F}(T)}\Bigg] + \cdots\\ &=& \int_{-\infty}^{E_{\rm F}(T)} E'D(E')\,dE' +\frac{\pi^2}{6}(k_{\rm B}T) D(E_{\rm F}(T))\\ &&\quad +\frac{\pi^2}{6}(k_{\rm B}T) E\frac{dD(E)}{dE}\big|_{E=E_{\rm F}(T)} + \cdots\quad \quad \quad\quad(1) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-cf56fadcbd2220aca6bd34da1ac3b2ed_l3.png)
第一項は
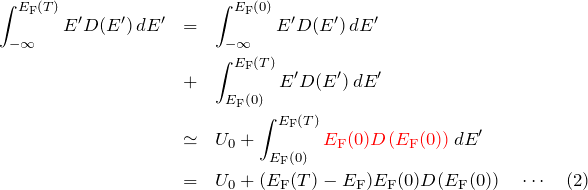
ここで ![]() K のときのフェルミレベル
K のときのフェルミレベル ![]() を用いて積分区間を
を用いて積分区間を
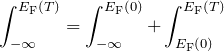
と変えた。また、![]() は
は ![]() K のときの内部エネルギーである。さらに、
K のときの内部エネルギーである。さらに、![]() の積分において、
の積分において、![]() が
が ![]() の値からほとんど変化しないとしてフェルミレベルでの値(定数)に置き換えている。したがって、被積分は定数となるため、積分は容易に実行される(4行目)。
の値からほとんど変化しないとしてフェルミレベルでの値(定数)に置き換えている。したがって、被積分は定数となるため、積分は容易に実行される(4行目)。
![]() のゾンマーフェルト展開
のゾンマーフェルト展開
![]()
を使用すると式(2)は
![]()
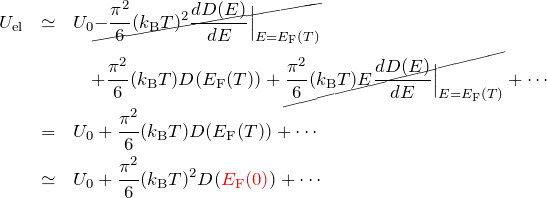
最後に、再度 ![]() Kでの値に置き換えた。
Kでの値に置き換えた。
電子比熱:内部エネルギーの温度微分
上で得られた結果を ![]() で微分して電子比熱
で微分して電子比熱 ![]() を得る。
を得る。
内部エネルギー ![]() として、以下のように電子の比熱
として、以下のように電子の比熱 ![]() が求められる。
が求められる。
![]()
たしかに電子被熱は温度 ![]() に比例する。 また、この形から、電子比熱は
に比例する。 また、この形から、電子比熱は ![]() K のときのフェルミレベルでの状態密度(状態数)に依存する ことがわかる。 このことからフェルミレベル近傍にあり、熱的に励起されている電子が比熱に寄与しているということからわかる。
K のときのフェルミレベルでの状態密度(状態数)に依存する ことがわかる。 このことからフェルミレベル近傍にあり、熱的に励起されている電子が比熱に寄与しているということからわかる。
自由電子における電子比熱
上の近似では状態密度 ![]() のみで電子比熱が記述できることがわかった。 自由電子における状態密度は、
のみで電子比熱が記述できることがわかった。 自由電子における状態密度は、
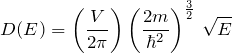
のように ![]() の1/2乗に比例する。
の1/2乗に比例する。 ![]() で定義されるフェルミ温度
で定義されるフェルミ温度 ![]() と全電子数
と全電子数 ![]() を用いて、
を用いて、
![]()
と書ける。これを用いて自由電子の電子比熱が求められる。