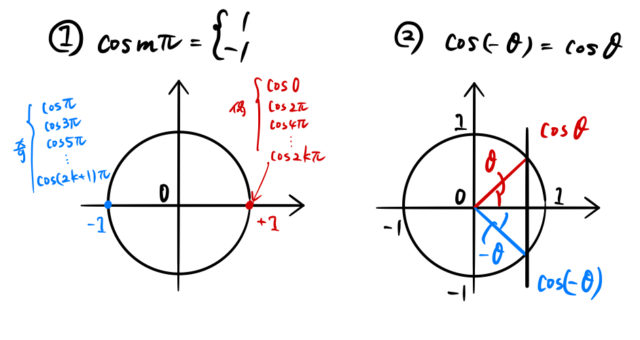
![]() の4乗のフーリエ級数を求める。
の4乗のフーリエ級数を求める。
例題
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ級数に展開せよ。
をフーリエ級数に展開せよ。
![]()
f(x)のグラフ
![]() のグラフは下のように周期的な
のグラフは下のように周期的な ![]() のグラフになる。
のグラフになる。
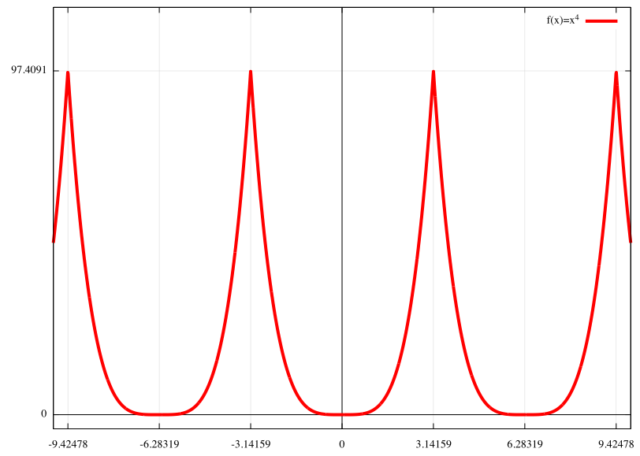
この関数は ![]() で偶関数である。
で偶関数である。
【解答】
周期関数 ![]() をフーリエ級数展開する。すなわち周期
をフーリエ級数展開する。すなわち周期 ![]() の様々な三角関数で展開する。
の様々な三角関数で展開する。
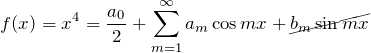
![]() が偶関数であるため、奇関数である
が偶関数であるため、奇関数である![]() のフーリエ係数 について
のフーリエ係数 について ![]() である。
である。
![]() について:
について:
![]() の両辺に
の両辺に ![]() をかけて、
をかけて、![]() で積分する。
で積分する。
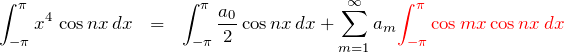
参考:三角関数の直交性から、![]() の積分は
の積分は ![]() のとき
のとき ![]() で、
で、![]() のとき
のとき ![]() になる。したがって、
になる。したがって、
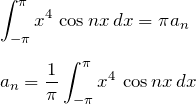
以下 積分計算(部分積分4回):
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_n&=&\frac{1}{\pi}\int_{-\pi}^{\pi}x^4\,\cos nx \, dx\\\\ &=&\frac{1}{\pi}\int_{-\pi}^{\pi}x^4\,\left(\frac{1}{n}\sin nx\right)'\, dx\\\\ &=&\frac{1}{n\pi}\left[x^4 \sin nx\right]_{-\pi}^{\pi} -\frac{4}{n\pi}\int_{-\pi}^{\pi}x^3 \,\sin nx \, dx\\\\ &=& 0-\frac{4}{n\pi}\int_{-\pi}^{\pi} x^3\,\left(-\frac{1}{n}\cos nx\right)'\, dx\\\\ &=& \frac{4}{n^2 \pi}\left\{\left[x^3 \cos nx\right]_{-\pi}^{\pi} -3\int_{-\pi}^{\pi} x^2 \,\cos nx \, dx \right\}\\\\ &=& \frac{4}{n^2 \pi}\left[\pi^3 \cos n\pi -(-\pi)^3 \cos(-n\pi)\right]\\\\ &&\quad-\frac{12}{n^2\pi}\int_{-\pi}^{\pi} x^2\,\left(\frac{1}{n}\sin nx\right)'\, dx\\\\ &=& \frac{4}{n^2 \pi}\cdot 2\pi^3 (-1)^n\\\\ &&\quad - \frac{12}{n^3 \pi}\left\{ \left[x^2 \sin nx\right]_{-\pi}^{\pi}- 2\int_{-\pi}^{\pi}x\,\sin nx \, dx \right\}\\\\ &=&\frac{8\pi^2(-1)^n}{n^2}\\\\ && -\frac{12}{n^3 \pi}\left\{0- 2\left[\frac{\sin nx}{n^2}-\frac{x\cos nx}{n}\right]_{-\pi}^{-\pi} \right\}\\\\ &=&\frac{8\pi^2(-1)^n}{n^2} -\frac{24}{n^3 \pi}\left(\frac{\pi}{n}\cos n\pi +\frac{\pi}{n}\cos n\pi\right)\\\\ &=&\frac{8\pi^2(-1)^n}{n^2}-\frac{48}{n^4}\,(-1)^n\\\\ &=& \textcolor{red}{\frac{8\pi^2(-1)^n}{n^2}\left\{1-\frac{6}{\pi^2 n^2}\right\}} \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-d0d301222d07f5b06268757259fc3e6c_l3.png)
この計算にはフーリエ級数でよく使う下の関係を利用した。
![]() について:
について:
![]() のフーリエ級数の式に
のフーリエ級数の式に ![]() をかけて
をかけて![]() で積分する。
で積分する。
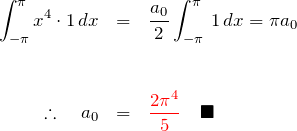
以上より、![]() をフーリエ級数に展開できる。
をフーリエ級数に展開できる。
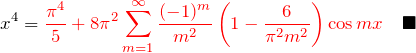
フーリエ級数で表したグラフ
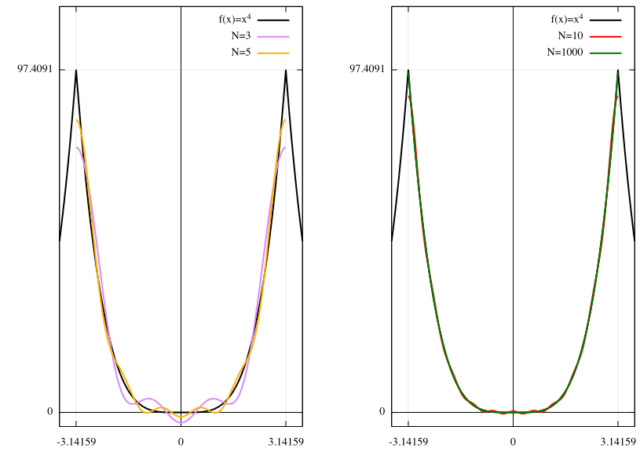
おまけ:フーリエ級数の和の部分を ![]() でなく有限の
でなく有限の ![]() で打ち切る。
で打ち切る。
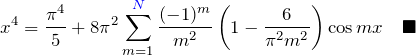
![]() で打ち切ったものと、もともとの
で打ち切ったものと、もともとの ![]() を下に示す。
を下に示す。
まとめ
![]() のフーリエ係数を4回の部分積分で求めてきた。
のフーリエ係数を4回の部分積分で求めてきた。