ゾンマーフェルト展開 (Sommerfeld expansion)は
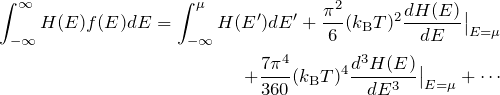
で表される。ここで、![]() はフェルミ分布関数
はフェルミ分布関数
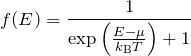
である。この展開を用いることで、有限温度における物性値を評価することができる。
たとえば、![]() とすれば有限温度における電子の内部エネルギーを計算できる。
とすれば有限温度における電子の内部エネルギーを計算できる。
* 積分区間の下限は ![]() でなく0になっているときもある(このとき、
でなく0になっているときもある(このとき、![]() のかわりに、
のかわりに、![]() とする)。
とする)。
ゾンマーフェルト展開の導出
導出はおもに微分・積分計算であるため、難しくはない。最後だけ難しい積分が出てくる。
関数を定義する
以下の計算に必要な関数を定義する。
![]() は扱いやすい関数とする。つまり、微分可能で
は扱いやすい関数とする。つまり、微分可能で ![]() となり、無限大で発散しないような関数を扱う (積分の下限が
となり、無限大で発散しないような関数を扱う (積分の下限が ![]() でなく 0 のときは、
でなく 0 のときは、![]() とする)。
とする)。
このような関数に対しては部分積分で積分を実行しやすくなる。また、フェルミ分布関数 ![]() については、
については、![]() ,
, ![]() であることを思い出しておこう。
であることを思い出しておこう。
また、微分すると ![]() になる関数
になる関数 ![]() を定義する
を定義する
![]()
部分積分をおこなう
部分積分を実行していこう。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-\infty}^\infty H(E)f(E)dE&=& \int_{-\infty}^\infty \frac{dG(E)}{dE}f(E)dE\\ &=& \Bigl[G(E)f(E) \Bigr]_{-\infty}^{\infty} -\int_{-\infty}^\infty G(E) \frac{df(E)}{dE} dE\\ &=& -\int_{-\infty}^\infty G(E) \frac{df(E)}{dE} dE \quad(\because G(-\infty)=0,\, f(\infty)=0)\quad\cdots \quad(1) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4ee3e56a5372a96262a0639df0ba110b_l3.png)
関数 ![]() は
は ![]() で発散しない関数であるため、第一項は0になっている。
で発散しない関数であるため、第一項は0になっている。
テイラー展開する
式(1)を計算するために、![]() を
を ![]() 周りで展開する。
周りで展開する。
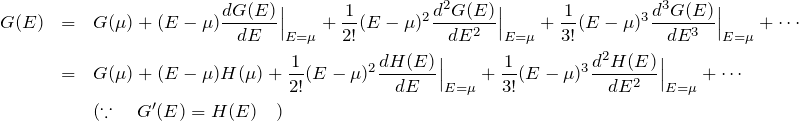
この結果を式(1)へ代入すると、
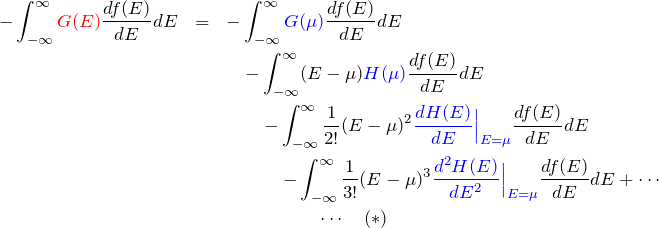
フェルミエネルギー ![]() はエネルギーに依存しないため、青色の項はエネルギー積分の外に出すことができる。 (
はエネルギーに依存しないため、青色の項はエネルギー積分の外に出すことができる。 (![]() などは
などは ![]() をエネルギーで微分した関数に対して、
をエネルギーで微分した関数に対して、![]() を代入するため、これも積分の外に出せる。)
を代入するため、これも積分の外に出せる。)
第一項:
![Rendered by QuickLaTeX.com \begin{eqnarray*} -\int_{-\infty}^\infty \textcolor{blue}{G(\mu)} \frac{df(E)}{dE} dE &=& -G(\mu)\Bigl[ f(E) \Bigr]_{-\infty}^{\infty}\\ &=& -G(\mu)(0-1) = +G(\mu) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8062f0f546e6ed63b41bfbf700e912f5_l3.png)
第二項以下(級数で表す):
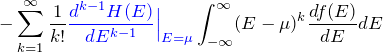
最後に示すようにフェルミ分布関数 ![]() の一階微分は
の一階微分は ![]() に対して偶関数である。 したがって、エネルギー積分内の被積分関数
に対して偶関数である。 したがって、エネルギー積分内の被積分関数
![]()
は、![]() に対して、
に対して、 ![]() が奇数のときに奇関数、
が奇数のときに奇関数、![]() が偶数のとき偶関数 になる。 したがって、
が偶数のとき偶関数 になる。 したがって、![]() の積分では偶関数の場合 (
の積分では偶関数の場合 (![]() が偶数) のみ積分が0ではない。
が偶数) のみ積分が0ではない。
これより、![]() に置き換えておく。
に置き換えておく。
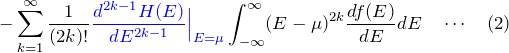
具体的に積分値を与える
エネルギー積分の部分を与える。まず、![]() に具体的な形(「フェルミ分布関数の微分」の章を参考)を代入する。
に具体的な形(「フェルミ分布関数の微分」の章を参考)を代入する。
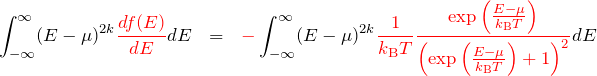
積分変数を以下のように置き換える。
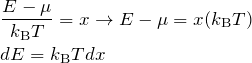
これより、積分は
![]()
となる。![]() の具体的な積分の値は
の具体的な積分の値は
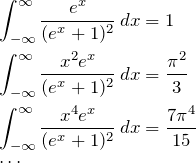
この結果と式(3)を用いて、式(2)を計算していく。
![Rendered by QuickLaTeX.com \begin{eqnarray*} && -\sum_{k=1}^{\infty} \frac{1}{(2k)!} \frac{d^{2k-1}H(E)}{dE^{2k-1}}\Big|_{E=\mu} \textcolor{red}{\int_{-\infty}^\infty (E-\mu)^{2k} \frac{df(E)}{dE} dE}\\ &=& -\sum_{k=1}^{\infty} \frac{1}{(2k)!} \frac{d^{2k-1}H(E)}{dE^{2k-1}}\Big|_{E=\mu} \left[\textcolor{red}{ -(k_{\rm B}T)^{2k}\int_{-\infty}^\infty \frac{x^{2k}e^x}{(e^x+1)^2} dx }\right]\\ &=& +(k_{\rm B}T)^2\frac{1}{2!}\frac{dH(E)}{dE}\Big|_{E=\mu} \textcolor{blue}{\int_{-\infty}^{\infty} \frac{x^2 e^x}{(e^x+1)^2}\,dx}\\ &&\quad +(k_{\rm B}T)^4\frac{1}{4!}\frac{d^3H(E)}{dE^3}\Big|_{E=\mu} \textcolor{blue}{\int_{-\infty}^{\infty} \frac{x^4 e^x}{(e^x+1)^2}\,dx} +\cdots \\ &=& +(k_{\rm B}T)^2\frac{1}{2}\frac{dH(E)}{dE}\Big|_{E=\mu} \cdot\textcolor{blue}{\frac{\pi^2}{3}}\\ &&\quad +(k_{\rm B}T)^4\frac{1}{24}\frac{d^3H(E)}{dE^3}\Big|_{E=\mu} \cdot \textcolor{blue}{\frac{7\pi^4}{15}} +\cdots \\ &=& +(k_{\rm B}T)^2\frac{\pi^2}{6}\frac{dH(E)}{dE}\Big|_{E=\mu}\\ &&\quad +(k_{\rm B}T)^4\frac{7\pi^4}{360}\frac{d^3H(E)}{dE^3}\Big|_{E=\mu} +\cdots \\ \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a8ae57637b1e323d561704495f9abe7b_l3.png)
これが式(*)の第二項以下になる。したがって、第一項の ![]() と合わせてゾンマーフェルト展開を得る。
と合わせてゾンマーフェルト展開を得る。
ゾンマーフェルト展開は以下で与えられる。
![]()
![]()
フェルミ分布関数の微分
途中で用いたフェルミ分布関数 ![]() の微分は容易に実行できる。
の微分は容易に実行できる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{df(E)}{dE}&=&\frac{d}{dE}\left[\frac{1}{\exp\left(\frac{E-\mu}{k_{\rm B}T}\right)+1}\right]\\ &=& -\frac{1}{k_{\rm B}T}\frac{\exp\left(\frac{E-\mu}{k_{\rm B}T}\right)}{\left(\exp\left(\frac{E-\mu}{k_{\rm B}T}\right)+1\right)^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-415acae9ebc7260c7f3ca7266e36af66_l3.png)