ゾンマーフェルト展開を用いて、化学ポテンシャル(フェルミレベル)![]() の温度依存性を求めていく。 最後に自由電子の場合の状態密度に対して、フェルミレベルの温度依存性を求めていく。
の温度依存性を求めていく。 最後に自由電子の場合の状態密度に対して、フェルミレベルの温度依存性を求めていく。
前提知識
ゾンマーフェルト展開
ゾンマーフェルト展開は以下で与えられる(【導出】)。
![]()
ここで、
![]()
導出
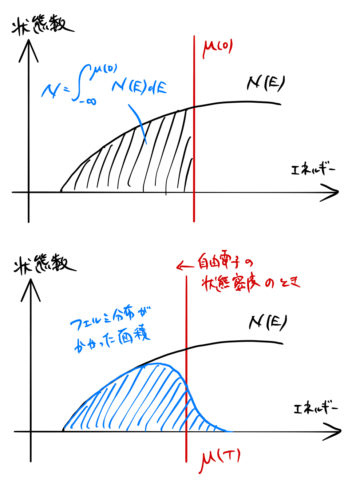
粒子数 ![]() が保存する条件のもと
が保存する条件のもと ![]() を計算していく。 以下では状態密度を
を計算していく。 以下では状態密度を ![]() と表す。
と表す。
粒子数Nを表す
粒子数 ![]() は保存するため、
は保存するため、![]() K での
K での ![]() を求める。
を求める。 ![]() Kのとき、フェルミ分布関数はフェルミレベル
Kのとき、フェルミ分布関数はフェルミレベル ![]() まで 1 である。 これより、粒子数
まで 1 である。 これより、粒子数 ![]() は
は
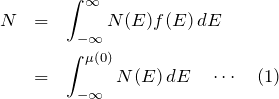
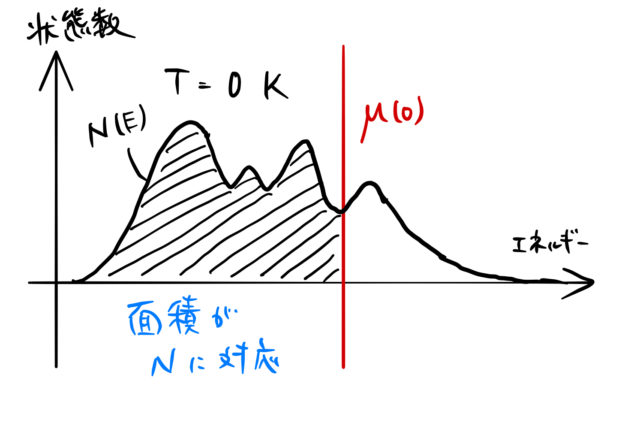
と表すことができる。つまり、下図の面積に対応する。
有限温度における粒子数Nの表現
粒子数 ![]() を有限温度の
を有限温度の ![]() により表すこともできる。
により表すこともできる。 ![]() を求める際に、有限温度の場合は
を求める際に、有限温度の場合は ![]() にフェルミ分布関数
にフェルミ分布関数 ![]() をかけて積分する必要がある。
をかけて積分する必要がある。
![]()
右辺にゾンマーフェルト展開を用いる。このとき、![]() である。 よって、
である。 よって、
![]()
である。したがって、ゾンマーフェルト展開の第二項までとって、
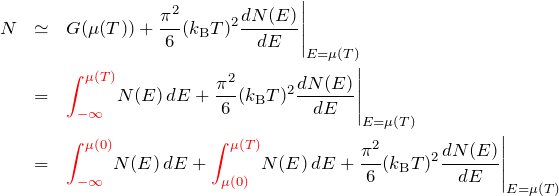
となる。積分は ![]() を経由しておこない、2つに分割している。 このように分割したときの第一項は式(1)の
を経由しておこない、2つに分割している。 このように分割したときの第一項は式(1)の ![]() に対応する。よって、
に対応する。よって、
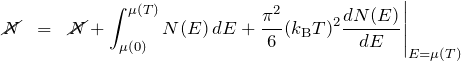
となる。
ここで、 エネルギーが ![]() から
から ![]() に変化する間、
に変化する間、![]() の値が変化しないものとする。 つまり、
の値が変化しないものとする。 つまり、![]() (定数)と近似すると、被積分関数は定数となるため、
(定数)と近似すると、被積分関数は定数となるため、
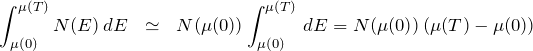
と積分を実行できる。また、
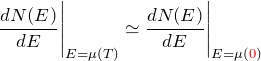
と近似する。
したがって、
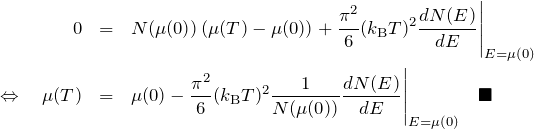
が得られる。![]() を
を ![]() で表すことができる。
で表すことができる。
![]() を状態密度
を状態密度 ![]() で表す。
で表す。
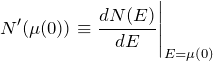
![]()
この式における状態密度 ![]() の形については、以下で説明するような自由電子の
の形については、以下で説明するような自由電子の ![]() に比例する形でなくてもよい。
に比例する形でなくてもよい。
自由電子におけるフェルミレベルの温度依存性
自由電子の状態密度は、
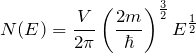
で表される。
これより、
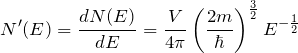
であり、
![]()
となる。
したがって、有限温度におけるフェルミレベル ![]() は
は
![]()
となる。
フェルミレベルが ![]() Kのときに比べて低いエネルギー側にシフトする理由は、状態密度
Kのときに比べて低いエネルギー側にシフトする理由は、状態密度 ![]() が
が ![]() に比例する増加関数であるからである。
に比例する増加関数であるからである。
フェルミ分布関数 ![]() は
は ![]() に対して対称な関数であるため、
に対して対称な関数であるため、![]() のまま
のまま ![]() を表すとする。このとき、図のように熱エネルギーにより空いた席
を表すとする。このとき、図のように熱エネルギーにより空いた席 ![]() と 埋まった席
と 埋まった席 ![]() の関係は
の関係は ![]() となる。 この大小関係は
となる。 この大小関係は ![]() が増加関数であるためである。
が増加関数であるためである。
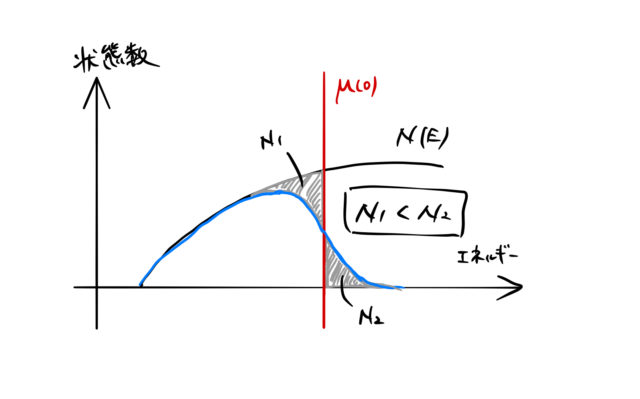
したがって ![]() で固定した場合には、粒子数は
で固定した場合には、粒子数は ![]() だけ増加するために、 フェルミレベルを低いエネルギー側(粒子数を減らす方向)にシフト させる必要がある。 このような理由から、式(2)の第二項が負で、フェルミレベルを押し下げる方向に働いている。
だけ増加するために、 フェルミレベルを低いエネルギー側(粒子数を減らす方向)にシフト させる必要がある。 このような理由から、式(2)の第二項が負で、フェルミレベルを押し下げる方向に働いている。
このように、自由電子の状態密度においては ![]() となっているが、一般的な傾向ではないことに注意する。
となっているが、一般的な傾向ではないことに注意する。