一次元のシュレディンガー方程式をポテンシャルがcos型になっている場合について解いていく。
一次元のシュレディンガー方程式
一次元の場合、時間に依存しないシュレディンガー方程式は
![]()
のように表すことができる。 ![]() の場合は自由電子模型と呼ばれ、
の場合は自由電子模型と呼ばれ、![]() は平面波
は平面波 ![]() の形で表される。 ここでは、
の形で表される。 ここでは、![]() でない場合についてシュレディンガー方程式を解いていく。
でない場合についてシュレディンガー方程式を解いていく。
cos型のポテンシャル
電子は結晶中で、原子による周期的なポテンシャルを受けると考えられる。 原子間隔を ![]() とすると、ポテンシャルには周期性
とすると、ポテンシャルには周期性 ![]() が現れる。このような具体的な状況をイメージしながら、
が現れる。このような具体的な状況をイメージしながら、![]() 形のポテンシャルの問題を見ていくとわかりやすい。
形のポテンシャルの問題を見ていくとわかりやすい。
ポテンシャルの形を与える
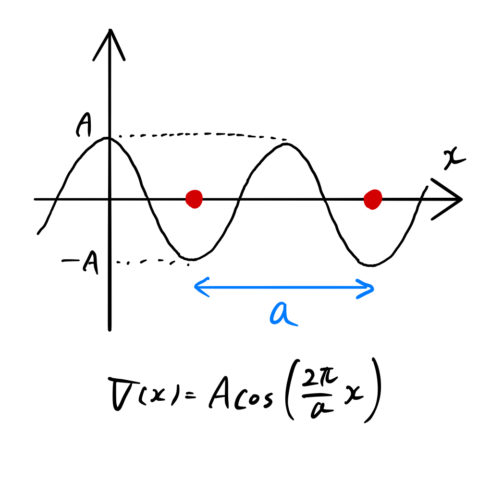
ここでは図のような周期 ![]() で変化する周期ポテンシャルを表すため、
で変化する周期ポテンシャルを表すため、
![]()
のような ![]() 型のポテンシャルを考える。
型のポテンシャルを考える。![]() はポテンシャルの振幅を表す。
はポテンシャルの振幅を表す。
シュレディンガー方程式は、
![]()
のように表すことができる。
変数変換をおこなう
簡単にするため、以下の変数変換をおこなう。
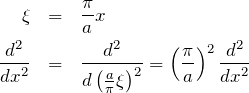
![]() の変換に応じて波動関数の形も
の変換に応じて波動関数の形も
![]()
としておく。
これよりシュレディンガー方程式は、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\left[ -\frac{\hbar^2}{2m}\left( \frac{\pi}{a} \right)^2 \frac{d^2}{d\xi^2}-A\cos(2\xi)-E \right]\tilde{\Phi}(\xi)=0\\ \Leftrightarrow\quad && \left[ \frac{d^2}{d\xi^2}+\frac{2m}{\hbar^2}\left(\frac{a}{\pi}\right)^2 A\cos(2\xi) +\frac{2m}{\hbar^2}\left(\frac{a}{\pi}\right)^2E \right]\tilde{\Phi}(\xi)=0\\ \Leftrightarrow\quad && \frac{d^2\tilde{\Phi}(\xi)}{d\xi^2} +\Big( \eta\cos(2\xi)+\varepsilon \Big)\tilde{\Phi}(\xi)=0\quad\cdots \quad (*) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6a575fed36bc58e673f6acdc70cc3c02_l3.png)
ここで、
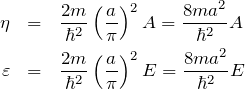
と置いた。![]() は
は ![]() に比例する。
に比例する。
シュレディンガー方程式を解く
![]() はポテンシャルの大きさと電子のエネルギーに関係する。
ここでは以下の2通りの場合を考える。
はポテンシャルの大きさと電子のエネルギーに関係する。
ここでは以下の2通りの場合を考える。
これはそれぞれ
- 運動エネルギーがポテンシャルの振幅より十分大きい場合
- ポテンシャルの振幅が運動エネルギーより十分大きい場合
に対応している。
(1) ![]() の場合:
の場合:
式(*)において、![]() の項を無視すると、
の項を無視すると、
![]()
この式は、![]() とした自由電子模型と同じシュレディンガー方程式の形をしており、波動関数の形は平面波の形であらわすことができる。
とした自由電子模型と同じシュレディンガー方程式の形をしており、波動関数の形は平面波の形であらわすことができる。
![]()
あるいは、
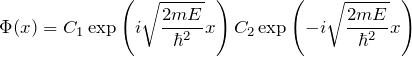
となる(![]() を計算する)。
を計算する)。
(2) ![]() の場合: この場合、ポテンシャルの項が重要になる。
の場合: この場合、ポテンシャルの項が重要になる。
![]()
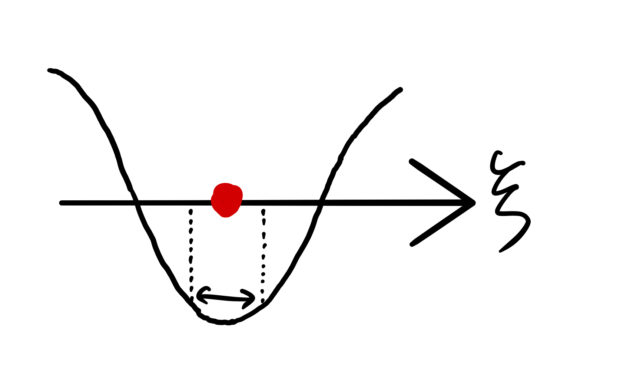
このとき、
![]()
と展開できるので、
![]()
となる。これは一次元調和振動子と同様の形をしている。 つまりは、![]() まわりの
まわりの ![]() 型ポテンシャルの展開は、バネと同じく変位
型ポテンシャルの展開は、バネと同じく変位 ![]() の2乗あるいは
の2乗あるいは ![]() の2乗に比例するポテンシャルを与える(下の「一次元調和振動子」を参考)。
の2乗に比例するポテンシャルを与える(下の「一次元調和振動子」を参考)。
したがって、エネルギーは
![]()
のように離散化される。連続的なエネルギー準位になるような、場合(1)の自由電子のときと異なる。
* 【一次元調和振動子のハミルトニアン】
シュレディンガー方程式は
![]()
であり、変数変換
![]()
により、
![]()
を得る。一次元調和振動子のエネルギーは
![]()
で表される。ここで、![]() は固有振動数である。また、波動関数
は固有振動数である。また、波動関数 ![]() はエルミート多項式で表すことができる。
はエルミート多項式で表すことができる。
** ![]() での展開は、図のような谷になっているポテンシャルにおいて、変位が微小であるような場合を考えることに対応する。 この時、平衡位置である谷底に物体を戻すような復元力が働いている系を考えるとよい。 この復元力は変位に比例する(フックの法則)。
での展開は、図のような谷になっているポテンシャルにおいて、変位が微小であるような場合を考えることに対応する。 この時、平衡位置である谷底に物体を戻すような復元力が働いている系を考えるとよい。 この復元力は変位に比例する(フックの法則)。
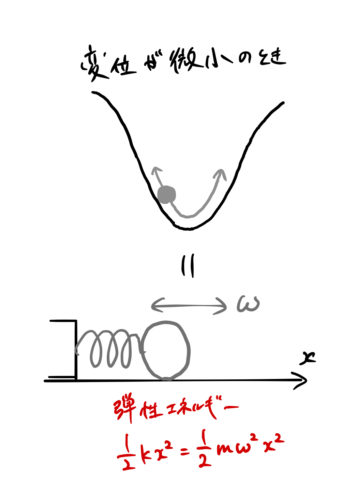
したがって、バネに繋がった物体を考えることと等価である。 このとき弾性エネルギー ![]() をポテンシャル
をポテンシャル ![]() として扱えば良い。 古典力学のハミルトニアンとの違いは、運動エネルギーを運動量演算子
として扱えば良い。 古典力学のハミルトニアンとの違いは、運動エネルギーを運動量演算子 ![]() を用いて
を用いて ![]() とすることである。
とすることである。
結果をまとめる
(1)(2)の場合をまとめると、
 のとき、自由電子のように扱える
のとき、自由電子のように扱える のとき、一次元調和振動子のように扱える
のとき、一次元調和振動子のように扱える
というようになる(下図)。
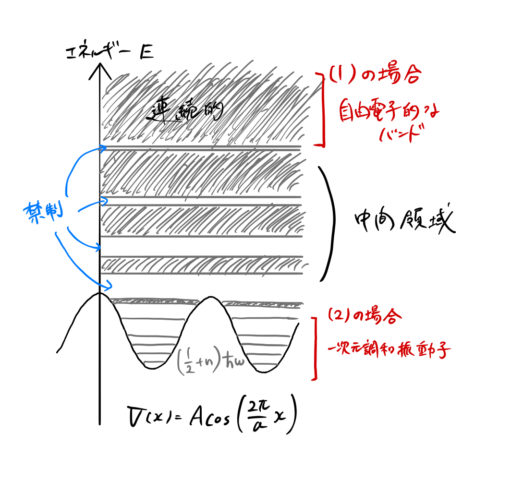
自由電子は平面波で表されているためバンドを形成する。 ポテンシャルの項が重要となる、エネルギー準位の低いときはエネルギーは量子化されている。 中間領域では、これらが混ざったようなエネルギーバンドが得られる。