電流の流れている針金に電流に垂直な磁場をかければローレンツ力を受けることはよく知られている。ホール効果は針金中を運動する電子のレベルでのローレンツ力が重要な鍵になる。ここではそのホール効果の基礎を簡単にまとめよう。
1. ホール効果でわかること
何によって半導体に電流が流れているかは、よく知られているように電子や正孔である。ここでいう正孔とは電子の抜け穴のようなもので正電荷をもつ。これらの電流の担い手をキャリアという。「キャリアが何なのか(電子か正孔か)」と「キャリアがどのくらいあるか(キャリア密度)」は半導体における重要な物性である。
これらを調べるためにホール効果が主に非磁性の半導体で応用されている。ホール効果の実験を測定することで主に以下の物性が測定できる。
- 半導体のキャリアの種類(電子か正孔か)
- 半導体のキャリア密度
キャリア密度が大きいほど電流が流れやすい、つまり抵抗は小さいだろう。
※ややこしいがホール効果のHallは人名で正孔のHoleとは何の関係もない![]() 。
。
2. ホール効果の実験
ここではキャリアは負電荷の電子であるとする。正孔の場合は、「2.3 キャリアの種類の特定」で考える。
2.1 ホール効果のかんたんな流れ
ホール効果で起こることを簡単にまとめておく。
- 電流の向き
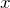 軸に垂直な
軸に垂直な  軸に磁場をかける
軸に磁場をかける - 電子は磁場によりローレンツ力をうける(電流と磁場に垂直な
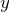 軸方向)
軸方向) 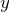 軸方向に電子の偏りができ、
軸方向に電子の偏りができ、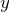 軸方向にホール電場ができる
軸方向にホール電場ができる 軸方向についてホール電場(横電場)とローレンツ力がつりあう
軸方向についてホール電場(横電場)とローレンツ力がつりあう
2.2 キャリア密度を測定
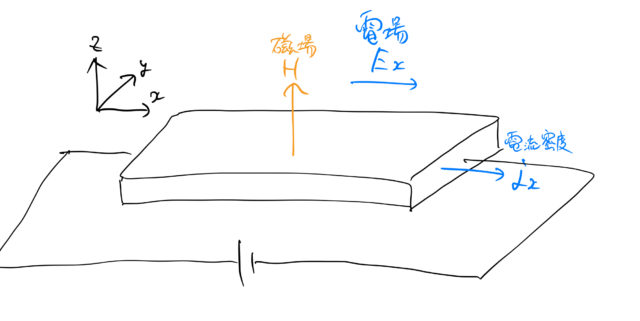
キャリア密度を測定するための手順を実験の模式図を使って説明する。
- 電流の向き
 軸に垂直な
軸に垂直な  軸に磁場をかける
軸に磁場をかける
2. 電子がローレンツ力をうける
電荷 ![]() をもった粒子が磁場
をもった粒子が磁場 ![]() 中
中 ![]() を速度
を速度 ![]() で運動すると以下のローレンツ力
で運動すると以下のローレンツ力 ![]() をうける。
をうける。
![]()
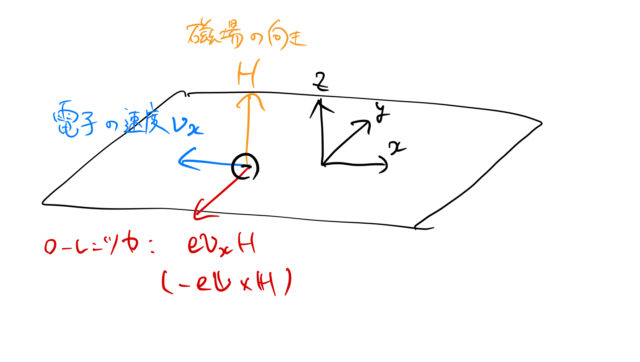
電子の場合は電流の向きと逆向きに運動する。この場合 ![]() 軸のマイナス方向に電子は速度をもつ。したがって、
軸のマイナス方向に電子は速度をもつ。したがって、![]() 軸の正の向きに磁場
軸の正の向きに磁場 ![]() がある場合のローレンツ力の向きは以下の通りである。つまり、
がある場合のローレンツ力の向きは以下の通りである。つまり、![]() から
から ![]() に右ネジを回す向きと逆向き(
に右ネジを回す向きと逆向き(![]() )である。
)である。
電子でなくて正孔の場合も ![]() の方向にローレンツ力を受けることに注意する(2.3「キャリアの種類の特定」を参照)。
の方向にローレンツ力を受けることに注意する(2.3「キャリアの種類の特定」を参照)。
3. ![]() 軸方向の電子の偏り
軸方向の電子の偏り
下図(上)のように、半導体の中の各電子が一様な磁場 ![]() からそれぞれローレンツ力を受ける。その結果、下図(下)のように電子が 手前(
からそれぞれローレンツ力を受ける。その結果、下図(下)のように電子が 手前(![]() 軸の負の向き)に集まり電子が偏る。
軸の負の向き)に集まり電子が偏る。
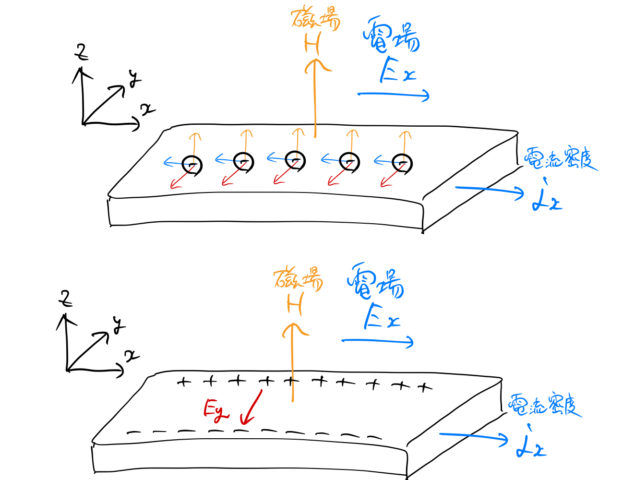
電子がローレンツ力により ![]() 方向に集まったため、
方向に集まったため、![]() 方向にはホール電場と呼ばれる横電場
方向にはホール電場と呼ばれる横電場 ![]() ができる。
ができる。
4. ホール電場(横電場)とローレンツ力のつり合い
電子は ![]() 方向に2つの力をうける。「横電場による力」と磁場による「ローレンツ力」である。ローレンツ力のほうが大きい場合は、電子は
方向に2つの力をうける。「横電場による力」と磁場による「ローレンツ力」である。ローレンツ力のほうが大きい場合は、電子は ![]() 方向に力をうけるため、
方向に力をうけるため、![]() 方向に電子が集まる。
方向に電子が集まる。![]() 方向に電子が増えれば横電場
方向に電子が増えれば横電場 ![]() は大きくなり、電子が受ける「横電場による力」も大きくなる。
は大きくなり、電子が受ける「横電場による力」も大きくなる。
したがって、下図のようにある段階で2つの力がつりあう。
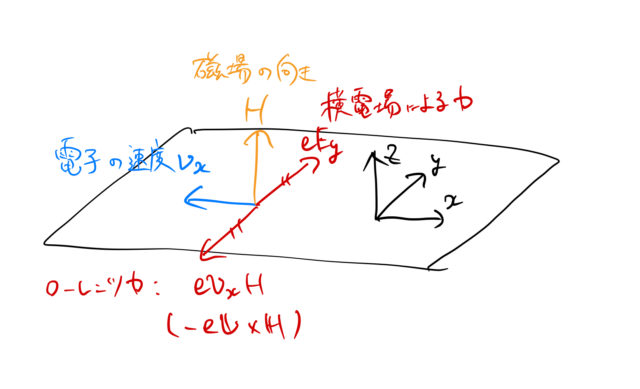
このとき、力のつり合いから
![]()
ここで、電子の速度 ![]() と電流密度
と電流密度 ![]() の関係は、
の関係は、
![]()
である。ここで ![]() はキャリア密度(電子の密度)、
はキャリア密度(電子の密度)、 ![]() は電荷素量 (
は電荷素量 (![]() )である。
)である。
この関係を用いて、
![]()
となる。この式の中で値がわかるものは電流密度 ![]() 、定数
、定数 ![]() 、かけた磁場の大きさ
、かけた磁場の大きさ ![]() である。したがって未知の値は
である。したがって未知の値は ![]() と キャリア密度
と キャリア密度 ![]() である。しかし、
である。しかし、![]() については下図のように
については下図のように ![]() 方向の電圧
方向の電圧 ![]() の測定値と
の測定値と ![]() 方向の試料の幅
方向の試料の幅 ![]() からわかる。
からわかる。
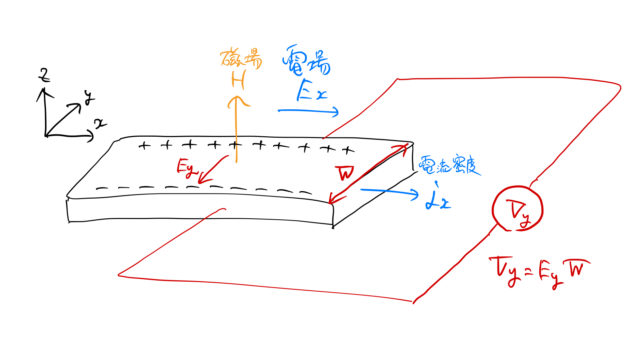
したがって、ホール効果の実験によってキャリア密度 ![]() がわかる。
がわかる。
![]()
電子の場合は ![]() であることに注意する。
であることに注意する。
2.3 キャリアの種類を特定
上の実験ではキャリアとして電子を扱った。正孔の場合は電荷が逆であるが、運動の向きも電子と逆になるためローレンツ力の向きは電子と同じである。
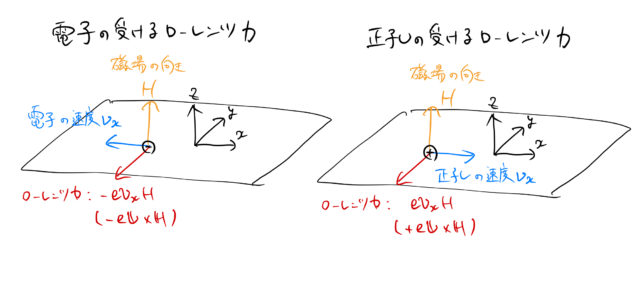
その結果、正孔は ![]() の方向へ運動するためにホール電場(横電場)
の方向へ運動するためにホール電場(横電場)![]() は電子の
は電子の ![]() と逆符号になる。したがって、
と逆符号になる。したがって、![]() 方向の電圧がプラスかマイナスか調べればキャリアが正孔か電子かわかる。
方向の電圧がプラスかマイナスか調べればキャリアが正孔か電子かわかる。
2.4 ホール係数
ホール効果の実験のまとめとして、最後にキャリア密度とキャリアの種類のために便利なホール係数 ![]() を定義する。
を定義する。
![]()
![]() の大きさからキャリア密度
の大きさからキャリア密度 ![]() がわかる。
がわかる。
また、![]() の符号によりキャリアの種類が特定できる。
の符号によりキャリアの種類が特定できる。
- 電子の場合:
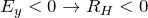
- 正孔の場合:
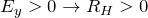
3. まとめ
ホール効果の実験により非磁性半導体のキャリア密度とキャリアの種類がわかる。この結果、考えている半導体が 「![]() 型半導体」か 「
型半導体」か 「![]() 型半導体」がわかる。このようにホール効果の実験は、半導体の物性を調べる上で非常に重要な実験である。
型半導体」がわかる。このようにホール効果の実験は、半導体の物性を調べる上で非常に重要な実験である。
非磁性でない場合、例えば強磁性体の場合はどうなるか。もともと内部磁場が存在しているため少々ややこしくなるだろう。この場合のホール効果については特に異常ホール効果という。
[1]:ホール効果はエポニム(wiki)である。Hallは人名でありHoleと発音も異なる。つまり、HallとHoleとはWhole differentである。
[2]:非磁性の場合は ![]() と
と ![]() の差が小さいためここでは
の差が小さいためここでは ![]() とした。
とした。