自由電子模型を用いてシュレディンガー方程式を解いていこう。 自由電子模型では電子が自由に動き回ることができる模型で、電子の受けるポテンシャルはゼロ(![]() )とする。 すなわち、シュレディンガー方程式(3次元)は、
)とする。 すなわち、シュレディンガー方程式(3次元)は、
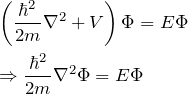
となる。解けそうな気がするだろう。
ここでは、系が無限に広い場合を解いていこう。 ほかのケースは以下の通り。
- 自由電子模型:無限に広い場合(3次元)←
- 自由電子模型:端がない周期的な系(1次元、3次元)
- 1次元井戸型ポテンシャル(無限井戸)
- 1次元井戸型ポテンシャル(有限井戸)
- 周期ポテンシャルのある場合(ブロッホの定理)
- クローニッヒ・ペニー模型
3次元:系が無限に広い場合
3次元の場合を考える。 シュレディンガー方程式を解いて、波動関数 ![]() を求めていこう。
を求めていこう。
![]()
シュレディンガー方程式を解く
初手が一番大事である。
ポイント
3変数関数の波動関数を,1変数関数の積で表す。
(1) ![]()
また、
![]()
であるから、式(1)は、
![]()
となる。両辺を ![]() で割ってやると、
で割ってやると、
![]()
左辺の3つの項はそれぞれ、![]() に依存する項、
に依存する項、![]() に依存する項、
に依存する項、![]() に依存する項に分かれている。そして、その和が右辺の定数
に依存する項に分かれている。そして、その和が右辺の定数 ![]() となる。 したがって、3つの項はそれぞれ定数となり、
となる。 したがって、3つの項はそれぞれ定数となり、![]() と置く。
と置く。
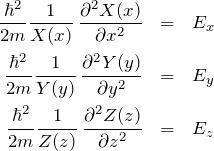
したがって、
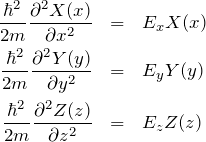
となる。同じ二階微分方程式が3つ得られた。 ![]() について解くと、
について解くと、
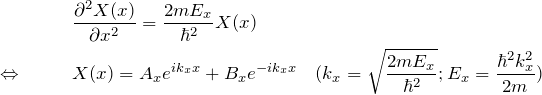
![]() も同様に、
も同様に、
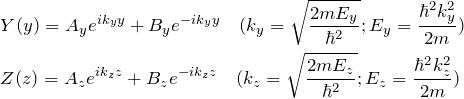
波動関数の形
したがって、式(2)より、
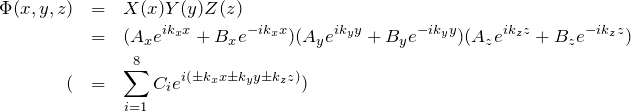
この場合、波動関数は平面波 ![]() の線型結合によって表すことができる。
の線型結合によって表すことができる。
エネルギーの形
また、エネルギーについては
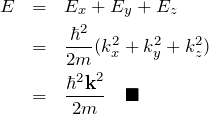
この波数 ![]() は
は ![]() であれば制限はない。 これは周期境界条件を課したときや1次元井戸型ポテンシャルの場合とは異なる。
であれば制限はない。 これは周期境界条件を課したときや1次元井戸型ポテンシャルの場合とは異なる。
まとめ
シュレディンガー方程式の解き方のうち、もっとも基本的な問題のひとつである。解き方をマスターしておいてほしい。