例題を使ってラプラス逆変換でよく使う「![]() 移動」について説明する。ここでは
移動」について説明する。ここでは ![]() などのラプラス逆変換については理解しているものとして進めていく。
などのラプラス逆変換については理解しているものとして進めていく。 ![]() 移動とは以下のような逆変換のことである。
移動とは以下のような逆変換のことである。
\\ (\quad F(s)&=&{\mathcal L}\left[f(t)\right](s) \quad) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1f6a66e6890276f6242ad855d16a8f92_l3.png)
式だけではわかりにくいので以下の例題を使って説明する。特に問題(4)(5)は間違えやすいので注意する。
次の![]() に関する関数をラプラス逆変換せよ。
に関する関数をラプラス逆変換せよ。
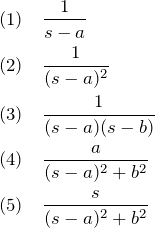
目次
1. s移動について
まず、![]() 移動がどこからきたか思い出そう。
移動がどこからきたか思い出そう。
exp(at) と t exp(at) のラプラス変換
![]() と
と![]() をラプラス変換せよ。
をラプラス変換せよ。
【解答】
&=&\int_0^{\infty} e^{at} e^{-st}\, dt\\ &=&\int_0^{\infty} e^{-(s-a)t}\, dt\\ &=&\left[-\frac{1}{s-a}\,e^{-(s-a)t}\right]_0^{\infty}\\ &=&\frac{1}{s-a}\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e362f21c3e022c3fc1060c7c0533dd82_l3.png)
また、
 &=&\int_0^{\infty} te^{at} e^{-st}\, dt\\ &=&\int_0^{\infty} te^{-(s-a)t}\, dt\\ &=&\int_0^{\infty} t\left(-\frac{1}{s-a}e^{-(s-a)t}\right)'\, dt\\ &=&\left[t\left(-\frac{1}{s-a}\,e^{-(s-a)t}\right)'\right]_0^{\infty} +\frac{1}{s-a}\int_0^{\infty} e^{-(s-a)t}\, dt\\ &=&\frac{1}{(s-a)^2}\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-572c8c4bc7752ce9657289fa28cdcd27_l3.png)
![]() によって、
によって、![]() となると考えられる。このことを、一般の
となると考えられる。このことを、一般の ![]() について確かめる。
について確かめる。
一般の f(t) と s移動
一般に、ラプラス変換後の![]() に対して
に対して ![]() とすると
とすると
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(\textcolor{red}{s})&=&{\mathcal L}[f(t)]=\int_0^{\infty} f(t)e^{- \textcolor{red}{s}t}\,dt\\ \rightarrow\quad F(\textcolor{red}{s-a})&=&\int_0^{\infty} f(t)e^{- \textcolor{red}{(s-a)}t}\,dt\\ &=&\int_0^{\infty} f(t)e^{at}\cdot e^{-st}\,dt\\ &=&{\mathcal L}[\textcolor{red}{e^{at}}f(t)\right](s) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-d12a806eaf274e6ead3701b3598a44c6_l3.png)
である。これが「![]() 移動」である。
移動」である。
s移動の使い方
![]() に対して、元の
に対して、元の ![]() に
に ![]() を掛けておけばよい。つまり、
を掛けておけばよい。つまり、
\\ (\quad F(s)&=&{\mathcal L}\left[f(t)\right](s) \quad) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-48f6ff24d28cfee73360d1ef8efee6f4_l3.png)
2. 【解答】
例題(1)(2)の解答/s移動の基本
![]() 移動を使って例題の(1)(2)を解く手順はカンタンである。 表記を簡単にするため、ラプラス変換・逆変換を「⇒」により表す。
移動を使って例題の(1)(2)を解く手順はカンタンである。 表記を簡単にするため、ラプラス変換・逆変換を「⇒」により表す。
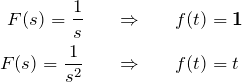
に対して ![]() として
として
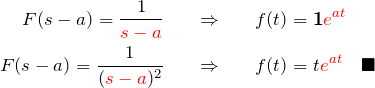
例題(3)の解答/部分分数分解してs移動
方針:部分分数分解する。
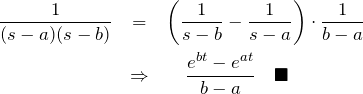
例題(4)(5)の解答/間違えやすいポイント
![]() のラプラス変換は、
のラプラス変換は、
\quad&\Rightarrow&\quad \frac{s}{s^2+b^2}=F(s)\\ {\mathcal L}\left[\sin b t\right](s)\quad&\Rightarrow&\quad \frac{b}{s^2+b^2}=F(s) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6292d46c3811f0799f66df61611cf72a_l3.png)
※![]() がどちらか覚えられない方:参考:ラプラス変換表と証明まとめ
がどちらか覚えられない方:参考:ラプラス変換表と証明まとめ
さて、この例題は自分がよく間違えていた問題である(戒め)。
【間違った解答】
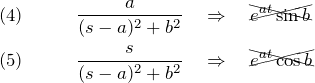
(4)は ![]() のラプラス変換の式が間違っている。(5)では「
のラプラス変換の式が間違っている。(5)では「![]() 移動」がうまくできていない。
移動」がうまくできていない。
【正しい解答】
例題(4)の方針:![]() を分子につくる!
を分子につくる!
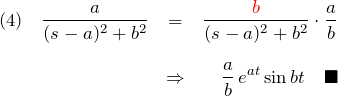
例題(5)の方針:![]() の形をつくる!
の形をつくる!
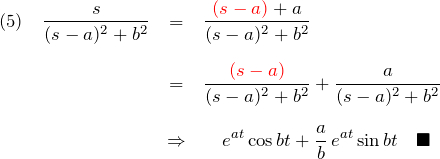
結局、
\\ \frac{b}{s^2+b^2}\quad&\Rightarrow&\quad{\mathcal L}\left[\sin b t\right](s) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f0681078d186b5589f9c24bb9b4f061e_l3.png)
に対して、
\\ \frac{b}{(\textcolor{red}{s-a})^2+b^2}\quad&\Rightarrow&\quad{\mathcal L}\left[\textcolor{red}{e^{at}}\sin b t\right](s) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4c2126ca33fec9ae44e7ad735fd9b073_l3.png)
となる。
3. まとめ
ラプラス逆変換するときには、この「![]() 移動」が使えるかどうかを考えるのがよいでしょう。ここではその例題と間違えやすいポイントをまとめました。ここで学んだ「s移動」とラプラス逆変換を習得すれば、微分方程式の初期値問題にも対応できる。
移動」が使えるかどうかを考えるのがよいでしょう。ここではその例題と間違えやすいポイントをまとめました。ここで学んだ「s移動」とラプラス逆変換を習得すれば、微分方程式の初期値問題にも対応できる。