金属中の電流密度 ![]() は電子密度
は電子密度 ![]() 、電荷
、電荷 ![]() 、電子の速度
、電子の速度 ![]() によって与えることができる。ここでは以下の式を導出する。さらに電気伝導度、オームの法則について簡単にまとめる。
によって与えることができる。ここでは以下の式を導出する。さらに電気伝導度、オームの法則について簡単にまとめる。
![]()
目次
1. 何が電流の大きさを決めるか
1.1 電流の単位
電流 ![]() の単位アンペア [A] は [C/t] である。つまり、1アンペアとは1秒間に1C(クーロン)だけ電荷(電子)が流れているということを表す。
の単位アンペア [A] は [C/t] である。つまり、1アンペアとは1秒間に1C(クーロン)だけ電荷(電子)が流れているということを表す。
ここでいう電流が大きいということは
- 1秒間に流れる電荷(電子)が多い
- そもそもの電荷 [C] が大きい
かである。「1. 1秒間に流れる電荷(電子)」を調べるために、「1秒間に電子が何個流れているか」を考える。電子を考えたこの時点で、「2. そもそもの電荷 [C] が大きい」は考えなくてい良い。なぜなら、電子1個の電気素量の大きさは ![]() によって定数で与えられているためである。
によって定数で与えられているためである。
したがって以下では、「1秒間に電子が何個流れているか」を考えよう。
1.2 電流密度を考えるのはなぜ?
次に「1秒間に電子が何個流れているか」は形状によるということを説明する。例として雨量を考える。「傘に当たる雨の量」と「家の屋根に当たる雨の量」の違いは面積の大きさの違いである。したがって、雨量の大小を比べたいのであれば面積当たりの量を考えるのが妥当である。
電流の場合も同様に、電流 ![]() より電流密度
より電流密度 ![]() を考えるほうが物性に近い。つまり同じ材質でも断面積が大きい針金にはたくさんの電子が流れるだろうから、形状の依存性は考えたくないために電流密度を考えるのである。電流密度の単位は [A/m
を考えるほうが物性に近い。つまり同じ材質でも断面積が大きい針金にはたくさんの電子が流れるだろうから、形状の依存性は考えたくないために電流密度を考えるのである。電流密度の単位は [A/m![]() ] である。
] である。
電流密度 ![]() は電流
は電流 ![]() を断面積
を断面積 ![]() で割ってやれば良い。
で割ってやれば良い。
![]()
1.3 電流密度は何に依存するか
形状の依存性は取り除いたため、電流密度 ![]() が何に依存するか考えよう。つまり「1秒間に電子が何個流れているか」を考える。
が何に依存するか考えよう。つまり「1秒間に電子が何個流れているか」を考える。
「単位面積あたりに通る電子数が大きい」のは、明らかに
- 電子が多い
- 電子の速さが大きい
場合だと考えらる。これらは下図のように電子密度 ![]() と電子の速度
と電子の速度 ![]() によって決定されそうである。
によって決定されそうである。
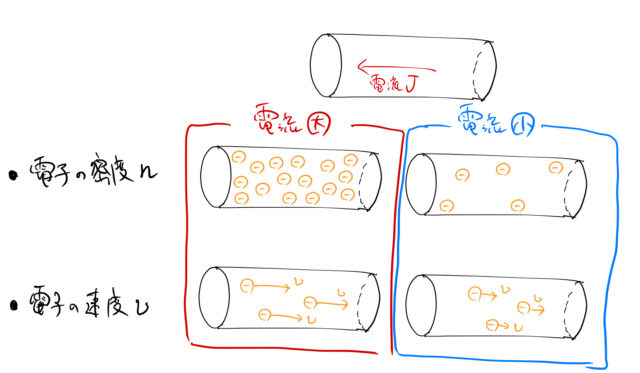
1.4 電流密度を計算する
確かに![]() が
が ![]() と
と ![]() に依存するか実際に計算してみる。以下では時間
に依存するか実際に計算してみる。以下では時間 ![]() の間に、断面積
の間に、断面積 ![]() あたりに通る電子数を考える。その後、電流を求めた後、断面積
あたりに通る電子数を考える。その後、電流を求めた後、断面積 ![]() で割って電流密度
で割って電流密度 ![]() を求める。
を求める。
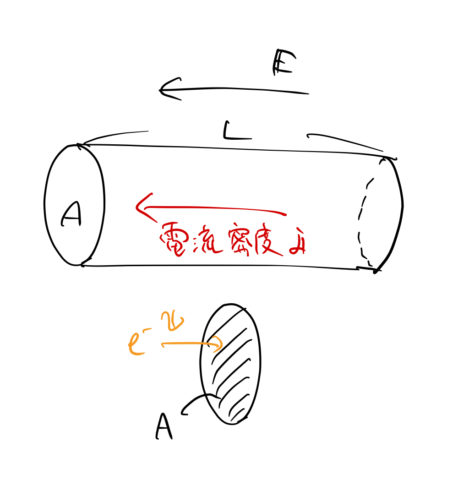
以下では単位をはっきりするために [m/t] などと書いている。
すべての電子が速度 ![]() [m/t] で図の右に動くとする。このとき、
[m/t] で図の右に動くとする。このとき、![]() 時間 [t]あたりに1個の電子は
時間 [t]あたりに1個の電子は![]() の向きに
の向きに ![]() [m] だけ進む。したがって、
[m] だけ進む。したがって、![]() [m
[m![]() ] を通る電子の数 [無次元] は単位体積あたりの電子密度
] を通る電子の数 [無次元] は単位体積あたりの電子密度 ![]() [1/m
[1/m![]() ] を用いて
] を用いて ![]() となる。
となる。
各電子は ![]() の電荷 [C] を運ぶため、電流
の電荷 [C] を運ぶため、電流 ![]() [A=C/t] と電流密度
[A=C/t] と電流密度 ![]() [A/m
[A/m![]() は
は
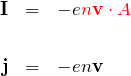
となる。確かに電流密度が電子密度と電子の速度に依存することがわかった。半導体の電子密度は実験的にホール効果などで測定できる。
2. オームの法則
![]() からオームの法則を求めていきたい。
からオームの法則を求めていきたい。
2.1 電子に速度vを与えるものは何か?
上では電子は勝手に速度 ![]() を持つとした。これはどこから来ているだろうか。
を持つとした。これはどこから来ているだろうか。
針金を用意した場合に、電場をかけていないなら電流はもちろん流れない。これは電子が完全に止まっているわけではなく、電子は様々な方向に運動しているが平均して速度が0ということである。
電場をかけた場合に電流が流れるのは、電子が電場から力を受けて平均して0でない力を受けるためである。そのため電子は平均して速度 ![]() となる。
となる。
電場 ![]() が図のようにある場合、電子は電場の向きと逆向きに力
が図のようにある場合、電子は電場の向きと逆向きに力 ![]() を受ける。
を受ける。
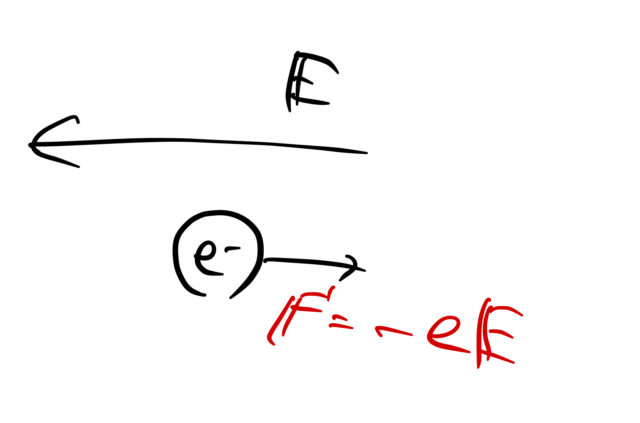
ここで電子の直線運動を考えたい。電子が他の電子と衝突したりすると直線運動ではなくなるため、電子が衝突するまでの時間を緩和時間として ![]() で表す。この
で表す。この ![]() の間は電子は直線的に運動しているとする。
の間は電子は直線的に運動しているとする。
この ![]() の間にうける電子の力積(力×時間)は、電子の平均的な運動量変化
の間にうける電子の力積(力×時間)は、電子の平均的な運動量変化 ![]() に一致する(運動量保存)。
に一致する(運動量保存)。
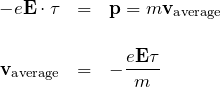
以上より、電場 ![]() によって電子が平均的に電場の向きと逆方向に速度
によって電子が平均的に電場の向きと逆方向に速度 ![]() をもつことがわかる。この電子の運動が電流となる。
をもつことがわかる。この電子の運動が電流となる。
以後、![]() を
を ![]() と考える。
と考える。
2.2 j=σE(σ:電気伝導度)
以上までの結果から
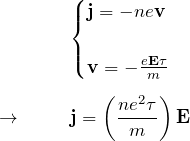
この式はかけた電場 ![]() に比例した電流密度
に比例した電流密度 ![]() が流れることを表す。この比例係数を
が流れることを表す。この比例係数を
![]()
と置いて電気伝導度とよぶ。電気伝導度は電流の流れやすさの指標になっていて、電流の流れにくさである比抵抗 ![]() の逆数で表される。
の逆数で表される。
まとめて書いておく。
![]()
2.3 オームの法則の導出
断面積 ![]() で長さ
で長さ ![]() の試料に電流
の試料に電流 ![]() が流れているとする。
が流れているとする。
「電流密度と電流の関係」と「電場と電圧の関係」から
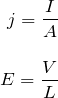
である。したがって、
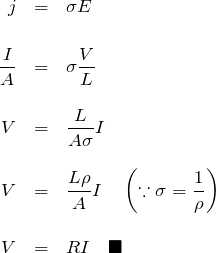
ここで抵抗 ![]() であり、試料の形状に依存する値であることが確認できる。また比抵抗である
であり、試料の形状に依存する値であることが確認できる。また比抵抗である ![]() は 2.2 に示したように形状に依存しない物性値である。
は 2.2 に示したように形状に依存しない物性値である。
以上より、電圧が電流に比例する「オームの法則」を得た。
![]()
抵抗 ![]() については、
については、
![]()
でも表すことができる。
2.4 抵抗Rと比抵抗ρの違い
念のため抵抗 ![]() と比抵抗
と比抵抗 ![]() の違いについて書いておく。これは質量と密度くらい違うということ。似たような話がいろいろな場面で出てくる。
の違いについて書いておく。これは質量と密度くらい違うということ。似たような話がいろいろな場面で出てくる。
物理では材料の形状による依存性を考えるのは面倒なので、形状の依存性のない物性値を扱うのが楽である。比抵抗 ![]() の場合は電子密度
の場合は電子密度 ![]() 、電子の(有効)質量
、電子の(有効)質量 ![]() 、緩和時間
、緩和時間 ![]() などの物性値で与えられ形状に依存しない。一方で、抵抗
などの物性値で与えられ形状に依存しない。一方で、抵抗 ![]() は材料の断面積
は材料の断面積 ![]() や長さ
や長さ ![]() などの形状に依存する。
などの形状に依存する。
- 抵抗
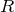 :断面積
:断面積 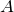 や長さ
や長さ 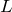 に依存
に依存 - 比抵抗
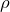 :断面積
:断面積 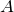 や長さ
や長さ 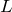 に依存しない
に依存しない
このくらいの違いがある。したがって、質量と密度くらい違う。
3. まとめ
金属の電気伝導の話からオームの法則までを導いた。よく問題で出されるようなのでおさえておきたいところ。