1. 解答
問題1: 線形代数
固有値 ![]()
![]()
固有ベクトル:
![]() のとき:
のとき:
![]()
![]()
ここで、
![]()
とおくと、
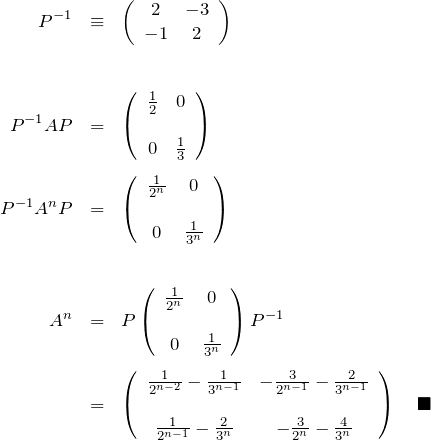
上の結果から、![]() のとき
のとき
![]()
である。ここで、
![]()
の両辺に左から ![]() をかけて
をかけて
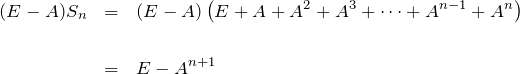
また、
![]()
より![]() の逆行列は存在する。したがって、左から
の逆行列は存在する。したがって、左から ![]() をかけて、
をかけて、
![]()
したがって、
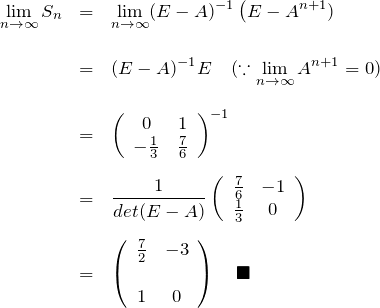
問題2:陰関数
![]() のとき:
のとき:
![]()
![]() のとき:
のとき:
![]()
極値は、
![Rendered by QuickLaTeX.com \begin{eqnarray*} y&=&0,\quad x=0\quad({\rm for}\quad t=0)\\\\ y&=&\sqrt[3]{4},\quad x=\sqrt[3]{2}\quad({\rm for}\quad t=\sqrt[3]{2})\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-676515c60ebb0886ef105db702eb9a0c_l3.png)
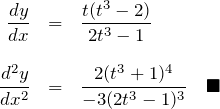
漸近線:
![]()
陰関数を図示:
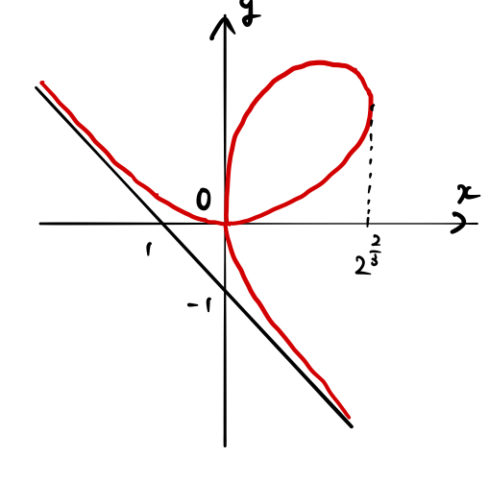
問題3:ラプラス変換
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty}e^{at} e^{-st}\, dt\\\\ &=& \int_0^{\infty}e^{(b+ci)t} e^{-(p+iq)t}\, dt \quad(a=b+ci,\; s=p+qi)\\\\ &=& \int_0^{\infty}e^{(p-b)+i(q-c)}t\, dt\\\\ &=& \left[ \frac{1}{-(p-b)-i(q-c)}\textcolor{red}{e^{-(p-b)t}}e^{-i(q-c)t} \right]_0^{\infty} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8e08a62cf8150763e3cc79f4d4003119_l3.png)
![]() は
は ![]() 、つまり、
、つまり、![]() のとき収束する。収束座標は
のとき収束する。収束座標は ![]() である。
である。
このとき、
![]()
積分のラプラス変換は「積分のラプラス変換(2通り)」にある。
積分方程式のラプラス変換は「積分方程式のラプラス変換の例題」にある。
問題4:複素平面
(1)
![]() は 「中心
は 「中心 ![]() 、半径1の円」
、半径1の円」![]()
(2)
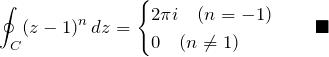
(3)
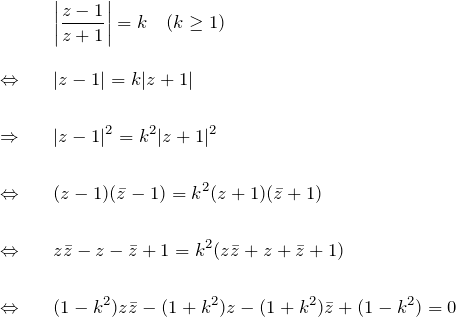
![]() のとき:
のとき:
![]()
となる。したがって ![]() は純虚数であり、虚軸を表す。
は純虚数であり、虚軸を表す。![]()
![]() のとき:
のとき:
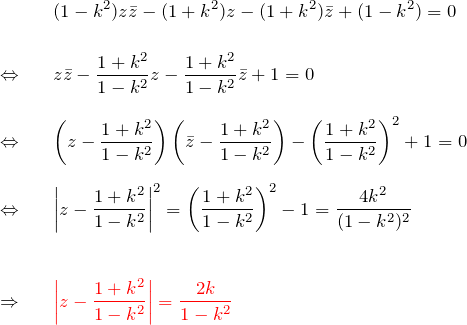
したがって、中心 ![]() 、半径
、半径 ![]() の円を表す。
の円を表す。![]()