![]() などの交換関係をまとめた。計算に必要なポイントは以下の通り。
などの交換関係をまとめた。計算に必要なポイントは以下の通り。
- 古典力学での角運動量
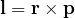 の形を使う
の形を使う - 量子力学では
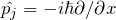 に注意
に注意 - 交換関係
![Rendered by QuickLaTeX.com [x_i,p_j]=i\hbar \delta_{ij}](https://batapara.com/wp-content/ql-cache/quicklatex.com-876d1dae638ad3bdf0872021c96f887f_l3.png) を利用( 導出 )
を利用( 導出 )
目次
1. 演算子の定義
lx, ly, lz の定義
量子力学で運動量演算子 ![]() を定義する。古典力学からの類推から、
を定義する。古典力学からの類推から、
![]()
を使う。量子力学では、位置演算子と運動量演算子は
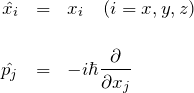
である(![]() 表示)。
表示)。
![]() の定義:
の定義:
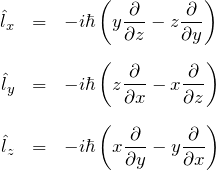
l^2 の定義
角運動量の大きさを表す演算子 ![]() を定義する。
を定義する。
![]()
昇降演算子 l+, l- の定義
![]() は角運動量を +1 したり-1 したりする。
は角運動量を +1 したり-1 したりする。
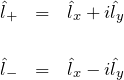
2. 交換関係(計算)
[ lx, ly ], [ ly, lz ], [ lz, lx ]
![]() と
と ![]() の交換関係を調べる。
の交換関係を調べる。
・![]() について:
について:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}_x\hat{l}_y &=&-\hbar^2\hbar\left(y\frac{\partial}{\partial z} -z\frac{\partial}{\partial y} \right) \hbar\left(z\frac{\partial}{\partial x} -x\frac{\partial}{\partial z} \right)\\\\ &=&-\hbar^2\Biggl[ \textcolor{red}{y\frac{\partial}{\partial z} \left(z\frac{\partial}{\partial x}\right)} + y\frac{\partial}{\partial z} \left(-x\frac{\partial}{\partial z}\right)\\\\ &&\quad - z\frac{\partial}{\partial y} \left(z\frac{\partial}{\partial x}\right) -z\frac{\partial}{\partial y} \left(x\frac{\partial}{\partial z}\right) \Biggr]\\\\ &=& -\hbar^2\left[ \textcolor{red}{y\frac{\partial}{\partial x} +yz\frac{\partial^2}{\partial z\partial x}} -xy\frac{\partial^2}{\partial z^2} -z^2\frac{\partial^2}{\partial x\partial y} +xz\frac{\partial^2}{\partial y\partial z} \right]\\\\ \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-fb2d004e4415da4c3200d1066589c4b7_l3.png)
赤色は注意すべき点。これは適当な関数 ![]() を用意してみればわかる。以下のように計算して、
を用意してみればわかる。以下のように計算して、![]() の係数を比べれば良い。
の係数を比べれば良い。
![Rendered by QuickLaTeX.com \begin{eqnarray*} y\frac{\partial}{\partial z}\left[ \left(z\frac{\partial}{\partial x}\right)\phi(x,y,z)\right] &=& y\frac{\partial}{\partial z}\left[ z\left(\frac{\partial \phi(x,y,z)}{\partial x}\right) \right] \\\\ &=& y\frac{\partial z}{\partial z}\frac{\partial \phi(x,y,z)}{\partial z} -yz\frac{\partial^2 \phi(x,y,z)}{\partial z^2}\\\\ &=& \left[y\frac{\partial z}{\partial z}\frac{\partial}{\partial z} -yz\frac{\partial^2}{\partial z^2}\right]\phi(x,y,z) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-49e15e04fe3d277c0668ab1ad01da6ed_l3.png)
・![]() について:
について:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}_x\hat{l}_y&=& -\hbar^2\left(z\frac{\partial}{\partial x} -x\frac{\partial}{\partial z}\right) \left(y\frac{\partial}{\partial z} -z\frac{\partial}{\partial y}\right)\\\\ &=& -\hbar^2\left[ yz\frac{\partial^2}{\partial x \partial z} -z^2\frac{\partial^2}{\partial x\partial y} -xy\frac{\partial^2}{\partial z^2} +\textcolor{red}{x\frac{\partial}{\partial y} +xz\frac{\partial^2}{\partial y\partial z}} \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-97249a0ff68f7b8a0e19725e8ee6e391_l3.png)
以上の結果から、
![Rendered by QuickLaTeX.com \begin{eqnarray*} [\hat{l}_x,\hat{l}_y]&=&\hat{l}_x\hat{l}_y-\hat{l}_y\hat{l}_x\\\\ &=& -\hbar^2\left(y\frac{\partial}{\partial x}-x\frac{\partial}{\partial y}\right)\\\\ &=&i\hbar \left[-i\hbar \left(x\frac{\partial}{\partial y}-y\frac{\partial}{\partial x}\right)\right]\\\\ &=& i\hbar \hat{l}_z\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-5879bb503599ef295c1c63d086434896_l3.png)
![]() も同様に計算できる。
も同様に計算できる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\hat{l}_x, \hat{l}_y\right]&=& i\hbar \hat{l}_z\\\\ \left[\hat{l}_y, \hat{l}_z\right]&=& i\hbar \hat{l}_x\\\\ \left[\hat{l}_z, \hat{l}_x\right]&=& i\hbar \hat{l}_y \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-94e1d2b52abdfae3405a62456b78a10e_l3.png)
[ l^2, lz ]
![]() と
と ![]() の交換関係を計算する。
の交換関係を計算する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} [\hat{l^2},\hat{l}_z] &=& [\hat{l}_x^2+\hat{l}_y^2+\hat{l}_z^2,\hat{l}_z]\\\\ &=& [\hat{l}_x^2,\hat{l}_z]+[\hat{l}_y^2,\hat{l}_z]+[\hat{l}_z^2,\hat{l}_z]\\\\ &=& [\hat{l}_x^2,\hat{l}_z]+[\hat{l}_y^2,\hat{l}_z]\quad(\because[\hat{l}_z,\hat{l}_z]=0) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-78083d7c0f63f8af80a55e94831d5c1c_l3.png)
![]() について:
について:
![Rendered by QuickLaTeX.com \begin{eqnarray*} [\hat{l}_x^2,\hat{l}_z]&=& \hat{l}_x^2\hat{l}_z-\hat{l}_z\hat{l}_x^2\\\\ &=& \hat{l}_x(\hat{l}_x \hat{l}_z) -(\hat{l}_z\hat{l}_x)\hat{l}_x\\\\ &=& \hat{l}_x(\hat{l}_z \hat{l}_x-i\hbar \hat{l}_y)- (\hat{l}_x \hat{l}_y+i\hbar \hat{l}_y)\hat{l}_x\\\\ &=& \cancel{\hat{l}_x\hat{l}_z\hat{l}_x} -i\hbar\hat{l}_x\hat{l}_y -\cancel{\hat{l}_x\hat{l}_z\hat{l}_x} -i\hbar\hat{l}_y\hat{l}_x\\\\ &=& -i\hbar\left[\hat{l}_x\hat{l}_y +\hat{l}_y\hat{l}_x \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8728722dc94cc00e0cf06113dfa8033b_l3.png)
![]() について:
について:
![Rendered by QuickLaTeX.com \begin{eqnarray*} [\hat{l}_y^2,\hat{l}_z]&=& \hat{l}_y^2\hat{l}_z-\hat{l}_z\hat{l}_y^2\\\\ &=& \hat{l}_y(\hat{l}_y \hat{l}_z) -(\hat{l}_z\hat{l}_y)\hat{l}_x\\\\ &=& \hat{l}_y(\hat{l}_z \hat{l}_y +i\hbar \hat{l}_x)- (\hat{l}_z \hat{l}_y -i\hbar \hat{l}_x)\hat{l}_y\\\\ &=& \cancel{\hat{l}_y\hat{l}_z\hat{l}_y} +i\hbar\hat{l}_y\hat{l}_x -\cancel{\hat{l}_y\hat{l}_z\hat{l}_y} +i\hbar\hat{l}_x\hat{l}_y\\\\ &=& +i\hbar\left[\hat{l}_x\hat{l}_y +\hat{l}_y\hat{l}_x \right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0b24c609bded404589c8f0040e0248c7_l3.png)
したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} [\hat{l^2},\hat{l}_z] &=&[\hat{l}_x^2,\hat{l}_z]+[\hat{l}_y^2,\hat{l}_z]+[\hat{l}_z^2,\hat{l}_z]\\\\ &=& -\cancel{i\hbar\left[\hat{l}_x\hat{l}_y +\hat{l}_y\hat{l}_x \right]} +\cancel{i\hbar\left[\hat{l}_x\hat{l}_y +\hat{l}_y\hat{l}_x \right]}+0\\\\ &=&0 \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-65b55f15448e8b9391f9210ed21b84a3_l3.png)
![]() についても同様に計算できる。
についても同様に計算できる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\hat{l^2},\hat{l}_x\right]&=&0\\\\ \left[\hat{l^2},\hat{l}_y\right]&=&0\\\\ \left[\hat{l^2},\hat{l}_z\right]&=&0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a00ce7f54b276730109ebaef0aad20c7_l3.png)
[ l^2, lz ]=0 の意味
この結果から、![]() と
と ![]() は同時固有状態をもつ。したがって、方位量子数方位量子数
は同時固有状態をもつ。したがって、方位量子数方位量子数 ![]() と磁気量子数
と磁気量子数 ![]() によって状態を表すことができる。そういうわけで、球面調和関数
によって状態を表すことができる。そういうわけで、球面調和関数 ![]() などで状態を表すことができる。
などで状態を表すことができる。
![]() は
は ![]() の
の ![]() 成分である。ここで、
成分である。ここで、![]() より、
より、![]() の
の ![]() 成分も決定できそうに見える。つまり、
成分も決定できそうに見える。つまり、![]() で指定した状態として
で指定した状態として ![]() を考えた代わりに、
を考えた代わりに、![]() とできるかどうかである。
とできるかどうかである。
しかし、それは許されない。なぜなら、
![]()
によって、![]() の
の ![]() 成分と
成分と ![]() 成分は同時に決定できない!
成分は同時に決定できない!
![]() の
の ![]() 成分のうち1つを決定してしまえば、他の2成分については決定できないのである。量子力学では慣例として、
成分のうち1つを決定してしまえば、他の2成分については決定できないのである。量子力学では慣例として、![]() の
の ![]() 成分を
成分を ![]() として扱っている。
として扱っている。
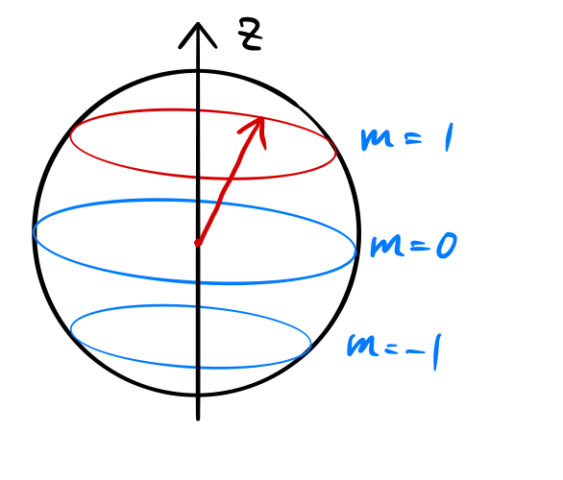
![]() と
と ![]() の
の ![]() 成分(
成分(![]() ) を決めると、
) を決めると、![]() という下の状態が与えられる。
という下の状態が与えられる。![]() の
の ![]() 成分は決定できないため、赤いベクトルはぐるぐる回る。
成分は決定できないため、赤いベクトルはぐるぐる回る。
3. l^2 を昇降演算子で表す
![]() について:
について:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}_+\hat{l}_- &=&(\hat{l}_x+i\hat{l}_y)(\hat{l}_x-i\hat{l}_y)\\\\ &=&\hat{l}_x^2 -i\hat{l}_x\hat{l}_y +i\hat{l}_y\hat{l}_x +\hat{l}_y^2\\\\ &=&\hat{l}_x^2+\hat{l}_y^2 -i[\hat{l}_x,\hat{l}_y]\\\\ &=&\hat{l}_x^2+\hat{l}_y^2 -i(i\hbar \hat{l}_z)\\\\ &=&\hat{l}_x^2+\hat{l}_y^2 +\hbar \hat{l}_z \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b37bda5f35dadd592402e329f5970deb_l3.png)
![]() について:
について:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}_-\hat{l}_+ &=&(\hat{l}_x-i\hat{l}_y)(\hat{l}_x+i\hat{l}_y)\\\\ &=&\hat{l}_x^2 +i\hat{l}_x\hat{l}_y -i\hat{l}_y\hat{l}_x +\hat{l}_y^2\\\\ &=&\hat{l}_x^2+\hat{l}_y^2 +i[\hat{l}_x,\hat{l}_y]\\\\ &=&\hat{l}_x^2+\hat{l}_y^2 +i(i\hbar \hat{l}_z)\\\\ &=&\hat{l}_x^2+\hat{l}_y^2 -\hbar \hat{l}_z \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-cde9b13a65be6f51003ebff75650dd6a_l3.png)
以上より、
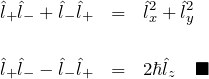
これより、![]() を 昇降演算子によって表すことができる。
を 昇降演算子によって表すことができる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}^2&=&\textcolor{red}{\hat{l}_x^2+\hat{l}_y^2}+\hat{l}_z^2\\\\ &=&\frac{1}{2}\left[\hat{l}_+\hat{l}_- + \hat{l}_-\hat{l}_+\right] +\hat{l}_z^2\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ab26e3d4714dc96836b09a64a76dbc9f_l3.png)
4. まとめ
簡単に結果をまとめておく
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\hat{l}_x, \hat{l}_y\right]&=& i\hbar \hat{l}_z\\\\ \left[\hat{l}_y, \hat{l}_z\right]&=& i\hbar \hat{l}_x\\\\ \left[\hat{l}_z, \hat{l}_x\right]&=& i\hbar \hat{l}_y \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-94e1d2b52abdfae3405a62456b78a10e_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\hat{l^2},\hat{l}_x\right]&=&0\\\\ \left[\hat{l^2},\hat{l}_y\right]&=&0\\\\ \left[\hat{l^2},\hat{l}_z\right]&=&0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a00ce7f54b276730109ebaef0aad20c7_l3.png)
![]()
軌道角運動量演算子の話は、同時固有状態のことに触れないとおもしろくないと思います。あと球面調和関数に作用させたときの話もここではしなかった。単なる計算まとめみたいになっている。